
| A. | $({-∞,-\frac{4}{3}}]$ | B. | $({-∞,\frac{3}{4}})$ | C. | $[{-\frac{3}{4},+∞})$ | D. | $[{-\frac{4}{3},+∞})$ |
分析 画出约束条件的可行域,利用目标函数的几何意义求解目标函数的期限分为即可.
解答 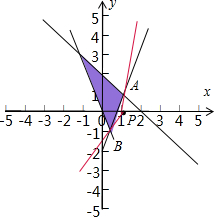 解:实数x,y满足$\left\{\begin{array}{l}x+y≤2\\ 2x+y≥0\\ 3x-y-2≤0\end{array}\right.$,的可行域如图:
解:实数x,y满足$\left\{\begin{array}{l}x+y≤2\\ 2x+y≥0\\ 3x-y-2≤0\end{array}\right.$,的可行域如图:
则$\frac{y}{1-x}$=$-\frac{y-0}{x-1}$,表示可行域内的点与P(1,0)连线的斜率的相反数,
由题意可知:$\left\{\begin{array}{l}{x+y=2}\\{3x-y-2=0}\end{array}\right.$,可得A(1,1),
$\left\{\begin{array}{l}{2x+y=0}\\{3x-y-2=0}\end{array}\right.$,可得B($\frac{2}{5}$,$\frac{-4}{5}$),
则$\frac{y}{1-x}$≥$\frac{-\frac{4}{5}}{1-\frac{2}{5}}$=-$\frac{4}{3}$.
故选:D.
点评 本题考查线性规划的应用,考查数形结合以及目标函数的几何意义,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=2x | B. | y2=4x | C. | y2=6x | D. | y2=8x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
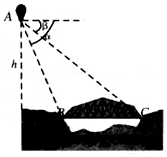 如图,从气球A上测得正前方的河流的两岸B、C的俯角分别为α=60°,β=45°,如果此时气球的高度h是10米,则河流的宽度BC=10-$\frac{10\sqrt{3}}{3}$米.
如图,从气球A上测得正前方的河流的两岸B、C的俯角分别为α=60°,β=45°,如果此时气球的高度h是10米,则河流的宽度BC=10-$\frac{10\sqrt{3}}{3}$米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
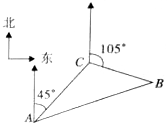 如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.
如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com