Question

20£®ÔÚƽÃæÖ±½Ç×ø±êϵxOyÖУ¬FÊÇÅ×ÎïÏßC£ºx²=2py£¨p£¾0£©µÄ½¹µã£¬MÊÇÅ×ÎïÏßCÉÏλÓÚµÚÒ»ÏóÏÞÄÚµÄÈÎÒâÒ»µã£¬¹ýM£¬F£¬OÈýµãµÄÔ²µÄÔ²ÐÄΪQ£¬µãQµ½Å×ÎïÏßCµÄ×¼ÏߵľàÀëΪ$\frac{3}{4}$£®¹ý¶¨µãD£¨0£¬p£©×÷Ö±ÏßÓëÅ×ÎïÏßCÏཻÓÚA£¬BÁ½µã£®
£¨I£©ÇóÅ×ÎïÏßCµÄ·½³Ì£»
£¨II£©ÈôµãNÊǵãD¹ØÓÚ×ø±êÔ­µãOµÄ¶Ô³Æµã£¬Çó¡÷ANBÃæ»ýµÄ×îСֵ£»
£¨¢ó£©ÊÇ·ñ´æÔÚ´¹Ö±ÓÚyÖáµÄÖ±Ïßl£¬Ê¹µÃl±»ÒÔADΪֱ¾¶µÄÔ²½ØµÃµÄÏÒ³¤ºãΪ¶¨Öµ£¿Èô´æÔÚ£¬Çó³ölµÄ·½³Ì£»Èô²»´æÔÚ£¬ËµÃ÷ÀíÓÉ£®

Answer 1

·ÖÎö £¨I£©ÒÀÌâÒâÖªF£¨0£¬$\frac{p}{2}$£©£¬ÓÉÌâÒâÖª$\frac{3p}{4}$=$\frac{3}{4}$£¬ÓÉ´ËÄÜÇó³öÅ×ÎïÏßCµÄ·½³Ì£®
£¨II£©ÒÀÌâÒâ¿ÉÖªµãNµÄ×ø±ê£¬¿ÉÉèA£¨x₁£¬y₁£©£¬B£¨x₂£¬y₂£©£¬Éè³öÖ±ÏßABµÄ·½³Ì£¬ÓëÅ×ÎïÏßÁªÁ¢ÏûÈ¥y£¬¸ù¾ÝΤ´ï¶¨ÀíÇóµÃx₁+x₂ºÍµÄx₁x₂±í´ïʽ£¬´úÈëÈý½ÇÐÎÃæ»ý¹«Ê½ÖУ¬¿ÉµÃk=0ʱ¡÷ANBÃæ»ýÓÐ×îСֵ£¬²¢ÇÒÇó³ö×îСֵ£®
£¨¢ó£©¼ÙÉèÂú×ãÌõ¼þµÄÖ±Ïßl´æÔÚ£¬Æä·½³ÌΪy=a£¬ÔòÒÔACΪֱ¾¶µÄÔ²µÄ·½³ÌΪ£¨x-0£©£¨x-x₁£©-£¨y-p£©£¨y-y₁£©=0£¬½«Ö±Ïß·½³Ìy=a´úÈëµÃx²-x₁x+£¨a-p£©£¨a-y₁£©=0£¬Ôò|x₁-x₂|²=4[a-$\frac{p}{2}$£©y₁+a£¨p-a£©]£®ÓÉ´ËÈëÊÖÄܹ»Çó³öÅ×ÎïÏßµÄͨ¾¶ËùÔÚµÄÖ±Ïߣ®

½â´ð ½â£º£¨I£©Å×ÎïÏßC£ºx²=2py£¨p£¾0£©µÄ½¹µãF£¨0£¬$\frac{p}{2}$£©£¬
Ô²ÐÄQÔÚÏ߶ÎOFµÄ´¹Ö±Æ½·ÖÏßy=$\frac{p}{4}$ÉÏ£®
ÒòΪÅ×ÎïÏßCµÄ×¼Ïß·½³ÌΪy=-$\frac{p}{2}$£¬
ËùÒÔ$\frac{3p}{4}$=$\frac{3}{4}$£¬¼´p=1£®
Òò´ËÅ×ÎïÏßCµÄ·½³ÌΪx²=2y£®
£¨II£©ÒÀÌâÒâµÃ£ºµãNµÄ×ø±êΪN£¨0£¬-1£©£¬¿ÉÉèA£¨x₁£¬y₁£©£¬B£¨x₂£¬y₂£©£¬
ÉèÖ±ÏßABµÄ·½³ÌΪy=kx+1£¬
Ö±Ïß·½³ÌÓëx²=2yÁªÁ¢£¬ÏûÈ¥yµÃx²-2kx-2=0£¬
ËùÒÔÓÉΤ´ï¶¨ÀíµÃx₁+x₂=2k£¬x₁x₂=-2£®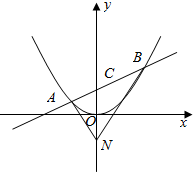

ÓÉͼ¿ÉµÃ£ºS_¡÷ABN=S_¡÷BCN+S_¡÷ACN=|x₁-x₂|=2$\sqrt{{k}^{2}+2}$£¬
¡àµ±k=0£¬£¨S_¡÷ABN£©_min=2$\sqrt{2}$£»
£¨¢ó£©¼ÙÉèÂú×ãÌõ¼þµÄÖ±Ïßl´æÔÚ£¬Æä·½³ÌΪy=a£¬ÔòÒÔACΪֱ¾¶µÄÔ²µÄ·½³ÌΪ£¨x-0£©£¨x-x₁£©+£¨y-p£©£¨y-y₁£©=0£¬
½«Ö±Ïß·½³Ìy=a´úÈëµÃx²-x₁x+£¨a-p£©£¨a-y₁£©=0£¬
Ôò|x₁-x₂|²=4[a-$\frac{p}{2}$£©y₁+a£¨p-a£©]£®
ÉèÖ±ÏßlÓëÒÔACΪֱ¾¶µÄÔ²µÄ½»µãΪP£¨x₃£¬y₃£©£¬Q£¨x₄£¬y₄£©£¬
ÔòÓÐ|PQ|²=|x₃-x₄|²=4[a-$\frac{p}{2}$£©y₁+a£¨p-a£©]£®
Áîa-$\frac{p}{2}$=0£¬µÃa=$\frac{p}{2}$£¬´Ëʱ|PQ|=pΪ¶¨Öµ£¬¹ÊÂú×ãÌõ¼þµÄÖ±Ïßl´æÔÚ£¬Æä·½³ÌΪy=$\frac{p}{2}$£¬
¼´Å×ÎïÏßµÄͨ¾¶ËùÔÚµÄÖ±Ïߣ®

µãÆÀ ±¾Ì⿼²éÅ×ÎïÏß·½³ÌµÄÇ󷨣¬¿¼²éÂú×ãÌõ¼þµÄµãÊÇ·ñ´æÔÚµÄÅжÏÓëÇ󷨣¬¿¼²é×ÛºÏÔËÓÃÊýѧ֪ʶ½øÐÐÍÆÀíÔËËãµÄÄÜÁ¦ºÍ½â¾öÎÊÌâµÄÄÜÁ¦£®