
分析 (1)利用零点的定义,f(x)=0即2x-$\frac{1}{{{2^{|x|}}}}$=0,讨论x值,去绝对值求解即可;
(2)化简得:(2t-$\frac{1}{{2}^{t}}$)(4t+1+m)≥0恒成立,根据t的范围可得4t+1+m≥0恒成立,只需求-(4t+1)的最大值;
(3)整理可得h(x)=2x[f(x)+a],构造函数h(t)=(t+$\frac{a}{2}$)2-$\frac{{a}^{2}}{4}$-1,利用二次函数性质,对对称轴讨论求出最小值.
解答 (本小题满分14分)
解:(1)f(x)=0即2x-$\frac{1}{{{2^{|x|}}}}$=0,
当x≥0时,2x-$\frac{1}{2^x}$=0,去分母得4x-1=0,∴x=0…(1分)
当x<0时,2x-$\frac{1}{{{2^{-x}}}}$=0恒成立,∴x<0…(3分)
综上:函数y=f(x)的零点的集合为{x|x≤0}…(4分)
(2)化简得:(2t-$\frac{1}{{2}^{t}}$)(4t+1+m)≥0恒成立,
∵t∈[1,2],
∴:2t-$\frac{1}{{2}^{t}}$>0,
∴4t+1+m≥0恒成立,
∴m≥-(4t+1),
∵-(4t+1)的最大值为-5,
∴m≥-5;
(3)h(x)=2x[f(x)+a]
=(2x)2+a2x-1,
令t=2x,1≤t≤4,
∴h(t)=(t+$\frac{a}{2}$)2-$\frac{{a}^{2}}{4}$-1,
当a<-8时,g(a)=h(4)=4a+15,
当-2>a≥-8时,g(a)=h(-$\frac{a}{2}$)=-$\frac{{a}^{2}}{4}$-1,
当a≥-2时,g(a)=h(1)=a.
点评 考查了函数零点的定义,恒成立问题和构造函数求闭区间二次函数的最小值.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
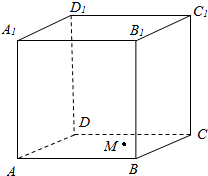 如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )| A. | 直线 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com