
����Ŀ��Ϊ�˽�ij����������ˮ����ţ�̵���֧�������빺��ʳƷ����֧�����õĹ�ϵ����������˸�����5����ͥ���õ�����ͳ�����ݱ���
����ʳƷ����֧������x����Ԫ�� | 2.09 | 2.15 | 2.50 | 2.84 | 2.92 |
����ˮ����ţ�̵���֧������y����Ԫ�� | 1.25 | 1.30 | 1.50 | 1.70 | 1.75 |
�����ϱ��ɵûع�ֱ�߷��� ![]() ������
������ ![]() ���ݴ˹��ƣ�������һ������ʳƷ����֧������Ϊ3.00��Ԫ�ļ�ͥ����ˮ����ţ�̵���֧������ԼΪ�� ��
���ݴ˹��ƣ�������һ������ʳƷ����֧������Ϊ3.00��Ԫ�ļ�ͥ����ˮ����ţ�̵���֧������ԼΪ�� ��
A.1.79��Ԫ
B.2.55��Ԫ
C.1.91��Ԫ
D.1.94��Ԫ
���𰸡�D
���������⣺���� ![]() =
= ![]() ����2.09+2.15+2.50+2.84+2.92��=2.50��
����2.09+2.15+2.50+2.84+2.92��=2.50�� ![]() =
= ![]() ����1.25+1.30+1.50+1.70+1.75��=1.50��
����1.25+1.30+1.50+1.70+1.75��=1.50��
�һع�ֱ�߷��� ![]() ��
�� ![]() ��
��
�� ![]() =1.5��0.85��2.5=��0.625��
=1.5��0.85��2.5=��0.625��
��ع鷽��Ϊ ![]() =0.85x��0.625��
=0.85x��0.625��
��x=3.00ʱ��![]() =0.85��3.00��0.625=1.925����Ԫ����
=0.85��3.00��0.625=1.925����Ԫ����
�ݴ˹��ƣ�������һ������ʳƷ����֧������Ϊ3.00��Ԫ�ļ�ͥ��
����ˮ����ţ�̵���֧������ԼΪ1.925��Ԫ��
��ѡ��D��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() .
.
��1����ʽ ![]() �Ľ⼯��
�Ľ⼯��
��2�������� ![]() �IJ���ʽ
�IJ���ʽ ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ ![]() ����ʵ��
����ʵ�� ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}��ǰn���ΪSn �� ��a3=3��S7=28���ڵȱ�����{bn}�У�b3=4��b4=8��
��1����an��bn��
��2��������{anbn}��ǰn���ΪTn �� ��Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�У���ADC= ![]() ��AB��CD��PC��ƽ��ABCD��CP=AB=2DC=2DA����E��BP�ϣ���EB=2PE��
��AB��CD��PC��ƽ��ABCD��CP=AB=2DC=2DA����E��BP�ϣ���EB=2PE�� 
��1����֤��DP��ƽ��ACE��
��2��������E��AC��P������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxoy�У�Բ�IJ�������Ϊ ![]() ����Ϊ��������������ԭ��OΪ���㣬x���������Ϊ����ļ�����ϵ�У�ֱ��l�ļ����귽��Ϊ
����Ϊ��������������ԭ��OΪ���㣬x���������Ϊ����ļ�����ϵ�У�ֱ��l�ļ����귽��Ϊ ![]() ��
��
��1����Բ�IJ������̻�Ϊ��ͨ���̣��ڻ�Ϊ�����귽�̣�
��2������P��ֱ��l�ϣ�����P��Բ�ľ�����Сʱ�����P�ļ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=ax3��x2��x+b��a��b��R��a��0����g��x��= ![]() ��e����Ȼ�����ĵ�������f��x����ͼ����x=��
��e����Ȼ�����ĵ�������f��x����ͼ����x=�� ![]() �������߷���Ϊy=
�������߷���Ϊy= ![]() ��
��
��1����a��b��ֵ��
��2��̽��ֱ��y= ![]() ���Ƿ�����뺯��g��x����ͼ�����У������ԣ�д���е�����꣬����˵�����ɣ�
���Ƿ�����뺯��g��x����ͼ�����У������ԣ�д���е�����꣬����˵�����ɣ�
��3��֤������x�ʣ����ޣ�2]ʱ��f��x����g��x����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�༶50��ѧ���Ŀ��Է���x�ֲ�������[50��100���ڣ������x�ķֲ�Ƶ����f��x����f��x��= 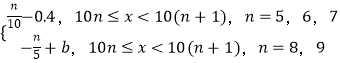 �����Գɼ����á�5���ơ����涨�����Է�����[50��60���ڵijɼ���Ϊ1�֣����Է�����[60��70���ڵijɼ���Ϊ2�֣����Է�����[70��80���ڵijɼ���Ϊ3�֣����Է�����[80��90���ڵijɼ���Ϊ4�֣����Է�����[90��100���ڵijɼ���Ϊ5�֣��÷ֲ�����ķ��������ڴӳɼ���1�֣�2�ּ�3�ֵ������÷ֲ����������6�ˣ��ٴ���6���г��3�ˣ�����3�˵ijɼ�֮��Ϊ�Σ���Ƶ����Ϊ���ʣ���
�����Գɼ����á�5���ơ����涨�����Է�����[50��60���ڵijɼ���Ϊ1�֣����Է�����[60��70���ڵijɼ���Ϊ2�֣����Է�����[70��80���ڵijɼ���Ϊ3�֣����Է�����[80��90���ڵijɼ���Ϊ4�֣����Է�����[90��100���ڵijɼ���Ϊ5�֣��÷ֲ�����ķ��������ڴӳɼ���1�֣�2�ּ�3�ֵ������÷ֲ����������6�ˣ��ٴ���6���г��3�ˣ�����3�˵ijɼ�֮��Ϊ�Σ���Ƶ����Ϊ���ʣ���
��1����b��ֵ�������ư༶�Ŀ���ƽ��������
��2����P����=7����
��3����εķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() sin��x+
sin��x+ ![]() ����
���� ![]() cos��x+
cos��x+ ![]() ����������x1 �� x2 �� x3 �� ����xn����0��x1��x2��x3������xn��6����|f��x1����f��x2��|+|f��x2����f��x3��|+��
����������x1 �� x2 �� x3 �� ����xn����0��x1��x2��x3������xn��6�У���|f��x1����f��x2��|+|f��x2����f��x3��|+�� ![]() ����n����СֵΪ�� ��
����n����СֵΪ�� ��
A.6
B.10
C.8
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ�����ף������ֲ�Ʒ������![]() ����ԭ�ϣ���֪����1��ÿ�ֲ�Ʒ����
����ԭ�ϣ���֪����1��ÿ�ֲ�Ʒ����![]() ԭ�ϼ�ÿ��ԭ�ϵĿ��������±���ʾ���������1�ּף��Ҳ�Ʒ�ɻ�����ֱ�Ϊ3��Ԫ��4��Ԫ�������ҵ�ɻ���������Ϊ__________��Ԫ.
ԭ�ϼ�ÿ��ԭ�ϵĿ��������±���ʾ���������1�ּף��Ҳ�Ʒ�ɻ�����ֱ�Ϊ3��Ԫ��4��Ԫ�������ҵ�ɻ���������Ϊ__________��Ԫ.
�� | �� | ԭ���� | |
A(��) | 3 | 2 | 12 |
B(��) | 1 | 2 | 8 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com