

���� ��1����A��-3��0����B��-1��0��������y=ax2+bx+3������ɣ�������ƽ��������������꼴�ɣ�
��2���䷽��ȷ���䶥�����꣬Ȼ������ƽ�ƹ���ȷ�������Ľ���ʽ��Ȼ������߶�����������Ψһ�Ĺ��������h��ֵ��ȡֵ��Χ���ɣ�
��3����������ƽ�ƣ���������ԭ��ʱ�������ʽΪy=x2����MN�Ľ���ʽΪy=kx+3��k��0������������������������ĵ�P��0��t������P��GH��x�ᣬ�ֱ��M��N��GH�Ĵ��ߣ�����ΪG��H�����ݡ�PMN��������y���ϣ��õ���GMP=��MPQ=��QPN=��HNP���Ӷ���GMP�ס�HNP���������������ζ�Ӧ�߳ɱ��������г��й�t�ķ�����⼴�ɣ�
���  �⣺��1��������y=ax2+bx+3����A��-3��0����B��-1��0������
�⣺��1��������y=ax2+bx+3����A��-3��0����B��-1��0������
��9a-3b+3=0��a-b+3=0
���a=1��b=4
�������ߵĽ���ʽΪy=x2+4x+3
��2���ɣ�1���䷽��y=��x+2��2-1
�������ߵĶ���M��-2��-1��
��ֱ��OM�Ľ���ʽΪy=$\frac{1}{2}$x
������ƽ�Ƶ������ߵĶ�������Ϊ��h��$\frac{1}{2}$h����
��ƽ�Ƶ������߽���ʽΪy=��x-h��2+$\frac{1}{2}$h����
�ٵ������߾�����Eʱ��
��C��0��9����
��h2+$\frac{1}{2}$h=9��
���h=$\frac{-1��\sqrt{145}}{4}$��
�൱$\frac{-1-\sqrt{145}}{4}$��h��$\frac{-1+\sqrt{145}}{4}$ʱ��ƽ�Ƶ����������߶�EFֻ��һ�������㣮
�ڵ����������߶�CDֻ��һ��������ʱ��
�ɷ�����y=��x-h��2+$\frac{1}{2}$h��y=-2x+9��
�� x2+��-2h+2��x+h2+$\frac{1}{2}$h-9=0��
���=��-2h+2��2-4��h2+$\frac{1}{2}$h-9��=0��
���h=4��
��ʱ������y=��x-4��2+2���߶�CDΨһ�Ĺ�����Ϊ��3��3�����������⣮
���ϣ�ƽ�Ƶ����������߶�CDֻ��һ��������ʱ��
����������ֵ��ȡֵ��Χ��h=4��$\frac{-1-\sqrt{145}}{4}$��h��$\frac{-1+\sqrt{145}}{4}$��
��3����������ƽ�ƣ���������ԭ��ʱ�������ʽΪy=x2��
��EF�Ľ���ʽΪy=kx+3��k��0����
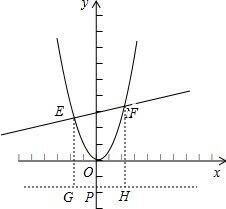
��������������������ĵ�P��0��t������P��GH��x�ᣬ�ֱ��E��F��GH�Ĵ��ߣ�����ΪG��H��
�ߡ�PEF��������y���ϣ�
���GEP=��EPQ=��QPF=��HFP��
���GEP�ס�HFP��
��$\frac{GP}{PH}=\frac{GE}{HF}$��
��$\frac{-{x}_{E}}{{x}_{F}}=\frac{{y}_{E}-t}{{y}_{F}-t}=\frac{k{x}_{E}+3-t}{k{x}_{F}+3-t}$
��2kxE•xF=��t-3����xE+xF��
��y=x2��y=kx+3����x2-kx-3=0��
��xE+xF=k��xE•xF=-3��
��2k��-3��=��t-3��k��
��k��0��
��t=-3��
��y��ĸ������ϴ��ڵ�P��0��-3����ʹ��PEF��������y���ϣ�
���� ������Ҫ�����˶��κ������ۺ�Ӧ���Լ����������ε�Ӧ�ã����κ������ۺ�Ӧ���dz��нε��ص������ر�ע���������ν�����ⲿ�ֿ�����ص�Ҳ���ѵ�ͬѧ��Ӧ�ص����գ�


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 360�� | B�� | 180�� | C�� | 120�� | D�� | 24�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 55 | B�� | 100 | C�� | 110 | D�� | 120 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com