
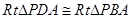 ,且
,且 ,
, 分别为
分别为 、
、 、
、 的中点
的中点
 的大小为
的大小为 ?若存在,求出CQ的长;若不存在,请说明理由。
?若存在,求出CQ的长;若不存在,请说明理由。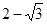 (3)
(3) 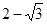
 EFGM共面,
EFGM共面,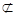 面EFG,EM
面EFG,EM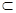 面EFG,得PB//平面EFG ………………4分
面EFG,得PB//平面EFG ………………4分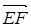 ="(1,0,0),"
="(1,0,0)," 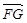 =(1,1,-1),
=(1,1,-1),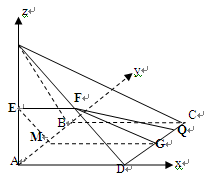
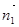 =(x,y,z)由
=(x,y,z)由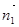
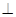
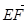 得出x="0," 由
得出x="0," 由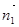
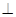
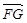 得出x+y-z=0
得出x+y-z=0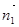 =(0,1,1),又
=(0,1,1),又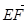 =(0,0,1),得cos
=(0,0,1),得cos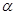 =
=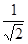 =
=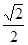 (
(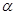 为
为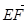 与
与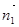 的夹角)
的夹角)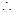
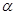 =45o ……………8分
=45o ……………8分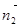 =(x,y,z),
=(x,y,z), =(2,b,-1)
=(2,b,-1)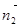
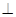
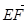 得出x="0," 由
得出x="0," 由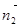
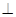
 得出2x+by-z=0,从而
得出2x+by-z=0,从而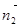 =(0,1,b)
=(0,1,b)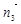 =(0,1,0),所以
=(0,1,0),所以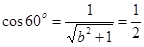 ,解得,b=
,解得,b=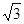
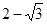 ……………12分
……………12分

 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:不详 题型:单选题
 ,则球的表面积( )
,则球的表面积( ) B、
B、 C、
C、 D、
D、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com