
【题目】已知二次函数![]() .
.
(1)若函数在区间![]() 上存在零点,求实数p的取值范围;
上存在零点,求实数p的取值范围;
(2)问是否存在常数![]() ,使得当
,使得当![]() 时,
时,![]() 的值域为区间D,且D的长度为
的值域为区间D,且D的长度为![]() .
.
(注:区间![]()
![]() 的长度为
的长度为![]() ).
).
【答案】(1)–20≤p≤12;(2)存在常数q= 8或q= 9,当x∈[q,10]时,![]() 的值域为区间
的值域为区间![]() ,且
,且![]() 的长度为12–q.
的长度为12–q.
【解析】
(1)利用零点存在性定理列出关于q的不等式,然后再利用不等式知识求解即可;(2)先利用单调性求出函数的值域,再利用区间长度列出关于q的方程,求解即可。
解:(1)∵二次函数f(x)=x2– 16x+p+ 3的对称轴是![]() ,∴函数
,∴函数![]() 在区间
在区间![]() 上单调递减,则函数
上单调递减,则函数![]() 在区间
在区间![]() 上存在零点须满足
上存在零点须满足![]() . ……………2分
. ……………2分
即(1 + 16 +p+ 3)(1 – 16 +p+ 3)≤0, 解得–20≤p≤12. …………………4分
⑵ 当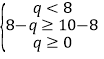 时,即0≤q≤6时,
时,即0≤q≤6时,
![]() 的值域为:[f(8),f(q)],即[p–61,q2–16q+p+ 3].
的值域为:[f(8),f(q)],即[p–61,q2–16q+p+ 3].
∴区间长度为q2– 16q+p+ 3 – (p– 61) =q2– 16q+ 64 =" 12" –q.
∴q2– 15q+ 52 =" 0" ∴![]() ,经检验
,经检验![]() 不合题意,舍去.……6分
不合题意,舍去.……6分
当 时,即6≤q<8时,
时,即6≤q<8时,![]() 的值域为:
的值域为:![]() ,即[p– 61,p– 57]
,即[p– 61,p– 57]
∴区间长度为p– 57 – (p– 61) =" 4" =" 12" –q∴q= 8.经检验q= 8不合题意,舍去. …8分
当q≥8时,![]() 的值域为:[f(q),f(10)],即 [q2– 16q+p+3,p– 57].
的值域为:[f(q),f(10)],即 [q2– 16q+p+3,p– 57].
∴区间长度为p– 57 –(q2– 16q+p+ 3) = –q2– 16q– 60 =" 12" –q,
∴q2– 17q+ 72 =" 0" , ∴q= 8或q= 9.经检验q= 8或q= 9满足题意.
所以存在常数q= 8或q= 9,当x∈[q,10]时,![]() 的值域为区间
的值域为区间![]() ,且
,且![]() 的长度为12–q. ………………………10分
的长度为12–q. ………………………10分


科目:高中数学 来源: 题型:
【题目】某班制定了数学学习方案:星期一和星期日分别解决![]() 个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”,则在一周中每天所解决问题个数的不同方案共有( )
个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”,则在一周中每天所解决问题个数的不同方案共有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥DABC中,ADDC,ACCB,AB=2AD=2DC=2,且平面ABD平面BCD,E为AC的中点.

(I)证明:ADBC;
(II)求直线 DE 与平面ABD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,已知矩形ABCD满足AB=5,![]() ,沿平行于AD的线段EF向上翻折(点E在线段AB上运动,点F在线段CD上运动),得到如图②所示的三棱柱
,沿平行于AD的线段EF向上翻折(点E在线段AB上运动,点F在线段CD上运动),得到如图②所示的三棱柱![]() .
.

⑴若图②中△ABG是直角三角形,这里G是线段EF上的点,试求线段EG的长度x的取值范围;
⑵若⑴中EG的长度为取值范围内的最大整数,且线段AB的长度取得最小值,求二面角![]() 的值;
的值;
⑶在⑴与⑵的条件都满足的情况下,求三棱锥A-BFG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C是矩形,平面ABC⊥平面AA1C1C,AB=2,AC=1,![]() ,
,![]() .
.

(1)求证:AA1⊥平面ABC;
(2)在线段BC1上是否存在一点D,使得AD⊥A1B?若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 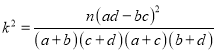 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系(
轴正半轴为极轴,建立极坐标系(![]() ),点
),点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 的延长线上,且满足
的延长线上,且满足![]() ,点
,点![]() 的轨迹为
的轨迹为![]() 。
。
(Ⅰ)求![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)设点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 面积的最小值。
面积的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com