
【题目】设函数f(x)=2ax2+2bx,若存在实数x0∈(0,t),使得对任意不为零的实数a,b均有f(x0)=a+b成立,则t的取值范围是_____.
【答案】![]()
【解析】
对任意不为零的实数![]() ,
,![]() 均有
均有![]() 成立等价于
成立等价于![]() ,分
,分![]() 或
或![]() 两种情况讨论,即可求出
两种情况讨论,即可求出![]() 的范围.
的范围.
f(x)=a+b成立等价于(2x﹣1)b=(1﹣2x2)a,
当x![]() 时,左边=0,右边≠0,不成立,
时,左边=0,右边≠0,不成立,
当x![]() 时,(2x﹣1)b=(1﹣2x2)a等价于
时,(2x﹣1)b=(1﹣2x2)a等价于![]() ,
,
设k=2x﹣1,则x![]() ,
,
则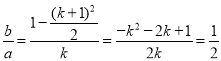 (
(![]() k﹣2),
k﹣2),
∵x∈(0,t),(t![]() ),或x∈(0,
),或x∈(0,![]() )∪(
)∪(![]() ,t),(t
,t),(t![]() ),
),
∴k∈(﹣1,2t﹣1),(t![]() ),或k∈(﹣1,0)∪(0,2t﹣1),(t
),或k∈(﹣1,0)∪(0,2t﹣1),(t![]() ),(*)
),(*)
∵a,b∈R,
∴![]() (
(![]() k﹣2),在(*)上恒有解,
k﹣2),在(*)上恒有解,
∴![]() (
(![]() k﹣2),在(*)上的值域为R,
k﹣2),在(*)上的值域为R,
设g(k)![]() (
(![]() k)﹣1,则g(k)在(﹣1,0),(0,2t-1)上单调递减,
k)﹣1,则g(k)在(﹣1,0),(0,2t-1)上单调递减,
对应值域为![]()
要保证![]() (
(![]() k﹣2)在(*)上的值域为R,则
k﹣2)在(*)上的值域为R,则
∴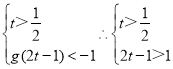 ,
,
解得t>1,
故答案为:![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为![]() .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(Ⅰ) 随机选取1件产品,求能够通过检测的概率;
(Ⅱ)随机选取3件产品,其中一等品的件数记为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)随机选取3件产品,求这三件产品都不能通过检测的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某闯关游戏规划是:先后掷两枚骰子,将此试验重复![]() 轮,第
轮,第![]() 轮的点数分别记为
轮的点数分别记为![]() ,如果点数满足
,如果点数满足![]() ,则认为第
,则认为第![]() 轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
(1)求第1轮闯关成功的概率;
(2)如果第![]() 轮闯关成功所获的奖金(单位:元)
轮闯关成功所获的奖金(单位:元) ![]() ,求某人闯关获得奖金不超过2500元的概率;
,求某人闯关获得奖金不超过2500元的概率;
(3)如果游戏只进行到第4轮,第4轮后无论游戏成功与否,都终止游戏,记进行的轮数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,AC与BD交于点O,PC⊥底面ABCD, 点E为侧棱PB的中点.
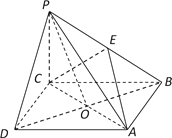
求证:(1) PD∥平面ACE;
(2) 平面PAC⊥平面PBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2) 若由线性回归方程得到的估计数据与4月份所选5天的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的. 请根据4月7日,4月15日与4月21日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判定所得的线性回归方程是否可靠?
,并判定所得的线性回归方程是否可靠?
参考公式: 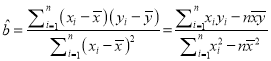 ,
, ![]()
参考数据: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com