
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
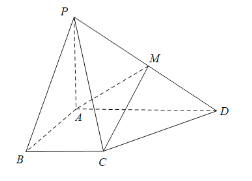
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)见解析(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明四边形
,证明四边形![]() 为平行四边形,即可证明
为平行四边形,即可证明![]() 平面
平面![]() .
.
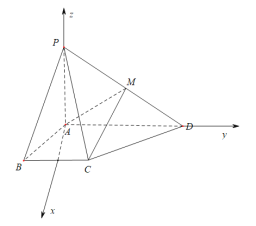
(2)以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系,求出平面
轴建立如图所示的空间直角坐标系,求出平面![]() 的一个法向量
的一个法向量![]() ,取平面
,取平面![]() 的一个法向量为
的一个法向量为![]() ,结合空间向量数量积运算即可得解.
,结合空间向量数量积运算即可得解.
证明:(1)如图,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
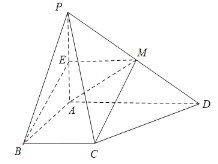
(2)在平面![]() 内过点
内过点![]() 作
作![]() 的垂线
的垂线![]() ,由题意知
,由题意知![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以
![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空
轴建立如图所示的空
间直角坐标系,由题意知![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则由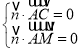 ,即
,即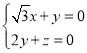 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
∴![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
∵![]() 底面
底面![]() ,∴可取平面
,∴可取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴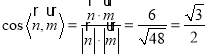 ,
,
∵二面角![]() 为锐二面角,
为锐二面角,
∴二面角![]() 的大小为
的大小为![]() .
.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
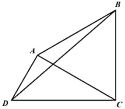
【题目】杭州西溪国家湿地公园是以水为主题的公园,以湿地良好生态环境和多样化湿地景观资源为基础的生态型主题公园.欲在该公园内搭建一个平面凸四边形![]() 的休闲观光及科普宣教的平台,如图所示,其中
的休闲观光及科普宣教的平台,如图所示,其中![]() 百米,
百米,![]() 百米,
百米,![]() 为正三角形.建成后
为正三角形.建成后![]() 将作为人们旅游观光休闲娱乐的区域,
将作为人们旅游观光休闲娱乐的区域,![]() 将作为科普宣教湿地功能利用弘扬湿地文化的区域.
将作为科普宣教湿地功能利用弘扬湿地文化的区域.
(1)当![]() 时,求旅游观光休闲娱乐的区域
时,求旅游观光休闲娱乐的区域![]() 的面积;
的面积;
(2)求旅游观光休闲娱乐的区域![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过焦点且垂直于
.过焦点且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 相交所得的弦长为3,直线
相交所得的弦长为3,直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,问直线
,问直线![]() 是否存在?若存在,求直线
是否存在?若存在,求直线![]() 的斜率
的斜率![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的五面体中,平面
为顶点的五面体中,平面![]() 平面
平面![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为60°,求平面
所成角为60°,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学计划用他姓名的首字母![]() ,身份证的后4位数字(4位数字都不同)以及3个符号
,身份证的后4位数字(4位数字都不同)以及3个符号![]() 设置一个六位的密码.若
设置一个六位的密码.若![]() 必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
A.864B.1009C.1225D.1441
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知衡量病毒传播能力的最重要指标叫做传播指数RO.它指的是,在自然情况下(没有外力介入,同时所有人都没有免疫力),一个感染到某种传染病的人,会把疾病传染给多少人的平均数.它的简单计算公式是:![]() 确认病例增长率
确认病例增长率![]() 系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确认病例的平均增长率为
系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确认病例的平均增长率为![]() ,两例连续病例的间隔时间的平均数为
,两例连续病例的间隔时间的平均数为![]() 天,根据以上RO数据计算,若甲得这种传染病,则
天,根据以上RO数据计算,若甲得这种传染病,则![]() 轮传播后由甲引起的得病的总人数约为( )
轮传播后由甲引起的得病的总人数约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程:
的参数方程: (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)过曲线![]() 上一点
上一点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,中点为
两点,中点为![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com