
【题目】4月23日是世界读书日,为提高学生对读书的重视,让更多的人畅游于书海中,从而收获更多的知识,某高中的校学生会开展了主题为“让阅读成为习惯,让思考伴随人生”的实践活动,校学生会实践部的同学随即抽查了学校的40名高一学生,通过调查它们是喜爱读纸质书还是喜爱读电子书,来了解在校高一学生的读书习惯,得到如表列联表:
喜欢读纸质书 | 不喜欢读纸质书 | 合计 | |
男 | 16 | 4 | 20 |
女 | 8 | 12 | 20 |
合计 | 24 | 16 | 40 |
(Ⅰ)根据如表,能否有99%的把握认为是否喜欢读纸质书籍与性别有关系?
(Ⅱ)从被抽查的16名不喜欢读纸质书籍的学生中随机抽取2名学生,求抽到男生人数ξ的分布列及其数学期望E(ξ).
参考公式:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
【题目】下列叙述正确的个数是( )
①若a>b,则ac2>bc2;
②若命题p为真命题题,命题q为假命题,则p∨q为假命题;
③若命题p:x0∈R,x ![]() ﹣x0+1≤0,则¬p:x∈R,x2﹣x+1>0.
﹣x0+1≤0,则¬p:x∈R,x2﹣x+1>0.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,已知2ccosA+a=2b
(1)求角C的值;
(2)若c=2,且△ABC的面积为 ![]() ,求a,b.
,求a,b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别是a,b,c,B是钝角,且 ![]() a=2bsinA.
a=2bsinA.
(1)求B的大小;
(2)若△ABC的面积为 ![]() ,且b=7,求a+c的值;
,且b=7,求a+c的值;
(3)若b=6,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三个内角A,B,C所对的边,且满足(2b﹣a)cosC=ccosA.
(Ⅰ)求角C的大小;
(Ⅱ)设![]() ,求y的最大值并判断当y取得最大值时△ABC的形状.
,求y的最大值并判断当y取得最大值时△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
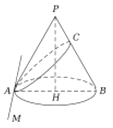
【题目】2000多年前,古希腊大数学家阿波罗尼奥斯((Apollonius)发现:平面截圆锥的截口曲线是圆锥曲线.已知圆锥的高为![]() ,
, ![]() 为地面直径,顶角为
为地面直径,顶角为![]() ,那么不过顶点
,那么不过顶点![]() 的平面;与
的平面;与![]() 夹角
夹角![]() 时,截口曲线为椭圆;与
时,截口曲线为椭圆;与![]() 夹角
夹角![]() 时,截口曲线为抛物线;与
时,截口曲线为抛物线;与![]() 夹角
夹角![]() 时,截口曲线为双曲线.如图,底面内的直线
时,截口曲线为双曲线.如图,底面内的直线![]() ,过
,过![]() 的平面截圆锥得到的曲线为椭圆,其中与
的平面截圆锥得到的曲线为椭圆,其中与![]() 的交点为
的交点为![]() ,可知
,可知![]() 为长轴.那么当
为长轴.那么当![]() 在线段
在线段![]() 上运动时,截口曲线的短轴顶点的轨迹为( )
上运动时,截口曲线的短轴顶点的轨迹为( )
A. 圆的部分 B. 椭圆的部分 C. 双曲线的部分 D. 抛物线的部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为:
的极坐标方程为: ![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数,
为参数, ![]() ).
).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,已知4sinA=4cosBsinC+bsin2C,且C≠ ![]() .
.
(1)求c;
(2)若C= ![]() ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com