
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面ABCD为菱形,E为棱PB的中点,O为AC与BD的交点,
(Ⅰ)证明:PD∥平面EAC
(Ⅱ)证明:平面EAC⊥平面PBD.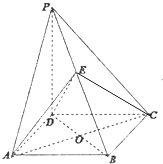
【答案】证明:(Ⅰ)∵ABCD是菱形,O是AC与BD的交点 ∴O是BD的中点;
连接EO.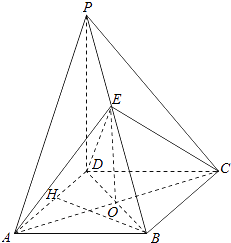
∵E是PB中点,O是BD的中点
∴EO∥PD.
根据直线与平面平行的判定定理可证明:
∴PD∥平面EAC.
(Ⅱ)∵PD⊥平面ABCD,AC平面ABCD,
∴AC⊥PD.∵四边形ABCD是菱形,∴AC⊥BD,
又∵PD∩BD=D,AC⊥平面PBD.
而AC平面EAC,∴平面EAC⊥平面PBD.
【解析】(Ⅰ)由已知得PD∥OE,利用直线与平面平行的判定定理证明即可.(Ⅱ)已知得AC⊥PD,AC⊥BD,由此能证明平面EAC⊥平面PBD.
【考点精析】通过灵活运用直线与平面平行的判定和平面与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知命题:“x∈{x|﹣1<x<1},使等式x2﹣x﹣m=0成立”是真命题.
(1)求实数m的取值集合M;
(2)设不等式 ![]() 的解集为N,若x∈N是x∈M的必要不充分条件,求实数a的取值范围.
的解集为N,若x∈N是x∈M的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为得到函数y=cos(x+ ![]() )的图象,只需将函数y=sinx的图象( )
)的图象,只需将函数y=sinx的图象( )
A.向左平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向右平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥E﹣ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC. (Ⅰ)证明:平面ABE⊥平面BCE;
(Ⅱ)求二面角A﹣DE﹣C的余弦值.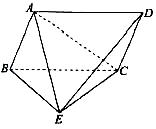
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生数学竞赛成绩的频率分布直方图如图所示,成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则该次数学成绩在[50,60)内的人数为( ) 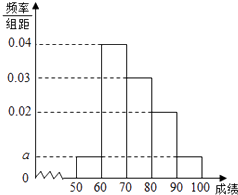
A.20
B.15
C.10
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,C> ![]() ,若函数y=f(x)在[0,1]上为单调递减函数,则下列命题正确的是( )
,若函数y=f(x)在[0,1]上为单调递减函数,则下列命题正确的是( )
A.f(cosA)>f(cosB)
B.f(sinA)>f(sinB)
C.f(sinA)>f(cosB)
D.f(sinA)<f(cosB)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且a5a6+a4a7=18,则log3a1+log3a2+…+log3a10=( )
A.5
B.9
C.log345
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x||x﹣1|<2},B={x|x2﹣2mx+m2﹣1<0}.
(1)当m=3时,求A∩B;
(2)若A∪B=A,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com