
【题目】已知函数![]() 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.
(1)求![]() 的取值范围.
的取值范围.
(2)设![]() 的两个极值点为
的两个极值点为![]() ,证明
,证明![]()
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)极值点转化为导函数零点,即![]() 在
在![]() 有两个不同根.变量分离为
有两个不同根.变量分离为![]() ,利用导数可得函数
,利用导数可得函数![]() 在
在![]() 上单调减,在
上单调减,在![]() 上单调增,根据趋势可得函数
上单调增,根据趋势可得函数![]() 在
在![]() 上范围为
上范围为![]() ,在
,在![]() 上范围为
上范围为![]() ,因此要有两解,需
,因此要有两解,需![]() ,(2)利用导数证明不等式关键是构造恰当的函数:
,(2)利用导数证明不等式关键是构造恰当的函数: ![]() 等价于
等价于![]()
![]() ,而由零点可得
,而由零点可得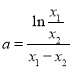 .代入化简得
.代入化简得![]() ,令
,令![]() ,则
,则![]() ,因此构造函数
,因此构造函数![]() ,利用导数求其最小值为
,利用导数求其最小值为![]() ,由于
,由于![]() ,所以命题得证.
,所以命题得证.
试题解析:(1)依题意,函数![]() 的定义域为
的定义域为![]() ,所以方程
,所以方程![]() 在
在![]() 有两个不同根.即方程
有两个不同根.即方程![]() 在
在![]() 有两个不同根.
有两个不同根.
转化为,函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点
上有两个不同交点
又![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上单调增,在
上单调增,在![]() 上单调减,从而
上单调减,从而![]() .
.
又![]() 有且只有一个零点是1,且在
有且只有一个零点是1,且在![]() 时,
时, ![]() ,在
,在![]() 时,
时, ![]() ,
,
所以由![]() 的图象,要想函数
的图象,要想函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,只需
上有两个不同交点,只需![]() ,即
,即![]()
(2)由(1)可知![]() 分别是方程
分别是方程![]() 的两个根,即
的两个根,即![]() ,
, ![]() ,
,
设![]() ,作差得,
,作差得, ![]() ,即
,即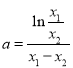 .
.
原不等式![]() 等价于
等价于
![]()
![]()
![]()
令![]() ,则
,则![]() ,
, ![]() ,
,
设![]() ,
, ![]() ,
, 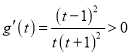 ,
,
∴函数![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,
即不等式![]() 成立,故所证不等式
成立,故所证不等式![]() 成立.
成立.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处. 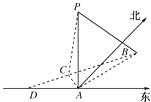
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).


(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的发展,移动支付(又称手机支付)越来越普通,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有![]() 个人.把这
个人.把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
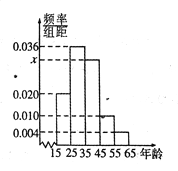
(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=sin(2x+ ![]() ),下列命题: ①函数图象关于直线x=﹣
),下列命题: ①函数图象关于直线x=﹣ ![]() 对称;
对称;
②函数图象关于点( ![]() ,0)对称;
,0)对称;
③函数图象可看作是把y=sin2x的图象向左平移个 ![]() 单位而得到;
单位而得到;
④函数图象可看作是把y=sin(x+ ![]() )的图象上所有点的横坐标缩短到原来的
)的图象上所有点的横坐标缩短到原来的 ![]() 倍(纵坐标不变)而得到;其中正确的命题是 .
倍(纵坐标不变)而得到;其中正确的命题是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点
,以极点为原点![]() ,极轴为
,极轴为![]() 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若用![]() 代换曲线
代换曲线![]() 的普通方程中的
的普通方程中的![]() 得到曲线
得到曲线![]() 的方程,若
的方程,若![]() 分别是曲线
分别是曲线![]() 和曲线
和曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com