
【题目】已知函数f(x)=loga(x+1),g(x)=loga ![]() ,(a>0且a≠1).记F(x)=2f(x)+g(x).
,(a>0且a≠1).记F(x)=2f(x)+g(x).
(1)求函数F(x)的零点;
(2)若关于x的方程F(x)﹣2m2+3m+5=0在区间[0,1)内仅有一解,求实数m的取值范围.
【答案】
(1)解:F(x)=2f(x)+g(x)= ![]() (a>0且a≠1),
(a>0且a≠1),
要使函数F(x)有意义,则必须 ![]() ,解得﹣1<x<1,
,解得﹣1<x<1,
∴函数F(x)的定义域为D=(﹣1,1).
令F(x)=0,则 ![]() …(*)
…(*)
方程变为 ![]() ,
,
∴(x+1)2=1﹣x,即x2+3x=0
解得x1=0,x2=﹣3,
经检验x=﹣3是(*)的增根,
∴方程(*)的解为x=0,
∴函数F(x)的零点为0
(2)解:函数 ![]() 在定义域D上是增函数,可得:
在定义域D上是增函数,可得:
①当a>1时,F(x)=2f(x)+g(x)在定义域D上是增函数,
②当0<a<1时,函数F(x)=2f(x)+g(x)在定义域D上是减函数.
因此问题等价于关于x的方程2m2﹣3m﹣5=F(x)在区间[0,1)内仅有一解.
①当a>1时,由(2)知,函数F(x)在[0,1)上是增函数,
∴F(x)∈[0,+∞),
∴只需2m2﹣3m﹣5≥0,解得:m≤﹣1,或 ![]() .
.
②当0<a<1时,由(2)知,函数F(x)在[0,1)上是减函数,
∴F(x)∈(﹣∞,0],
∴只需2m2﹣3m﹣5≤0解得: ![]() ,
,
综上所述,当0<a<1时: ![]() ;
;
当a>1时,m≤﹣1,或 ![]()
【解析】(1)利用对数函数和分式函数的定义域即可得出F(x)其定义域,利用零点的意义和对数函数的单调性即可得出;(2)对a分类讨论可得函数F(x)的单调性,进而问题等价于关于x的方程2m2﹣3m﹣5=F(x)在区间[0,1)内仅有一解.再利用一元二次不等式的解法即可得出.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】如图,在棱长为3的正方体ABCD﹣A1B1C1D1中,A1E=CF=1. 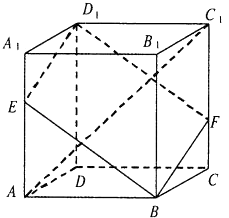
(1)求两条异面直线AC1与D1E所成角的余弦值;
(2)求直线AC1与平面BED1F所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=2sin(3x﹣ ![]() ),有下列命题:①其表达式可改写为y=2cos(3x﹣
),有下列命题:①其表达式可改写为y=2cos(3x﹣ ![]() );②y=f(x)的最小正周期为
);②y=f(x)的最小正周期为 ![]() ;③y=f(x)在区间(
;③y=f(x)在区间( ![]() ,
, ![]() )上是增函数;④将函数y=2sin3x的图象上所有点向左平行移动
)上是增函数;④将函数y=2sin3x的图象上所有点向左平行移动 ![]() 个单位长度就得到函数y=f(x)的图象.其中正确的命题的序号是(注:将你认为正确的命题序号都填上).
个单位长度就得到函数y=f(x)的图象.其中正确的命题的序号是(注:将你认为正确的命题序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,A(a,0),B(0,b),O(0,0),△OAB的面积为1.
,A(a,0),B(0,b),O(0,0),△OAB的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P是椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N.求证:|AN||BM|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,首项a1=1,公比q>0,其前n项和为Sn,且S1+a1,S3+a3,S2+a2成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足![]() ,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(﹣1,1)上的函数f(x)满足: ![]() ,当x∈(﹣1,0)时,有f(x)>0,且
,当x∈(﹣1,0)时,有f(x)>0,且 ![]() .设
.设 ![]() ,则实数m与﹣1的大小关系为( )
,则实数m与﹣1的大小关系为( )
A.m<﹣1
B.m=﹣1
C.m>﹣1
D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com