
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,(i)求曲线
时,(i)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(ii)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,求证:
,求证: ![]() .
.
【答案】(Ⅰ)(i)![]() ,(ii)递增区间是
,(ii)递增区间是![]() ,递减区间是
,递减区间是![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】试题分析:(Ⅰ)(i)求出![]() ,求出
,求出![]() 的值可得切点坐标,求出
的值可得切点坐标,求出![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(ii)分别令
处的切线方程;(ii)分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(Ⅱ)先利用导数证明
的减区间;(Ⅱ)先利用导数证明![]() ,则
,则![]() ,再利用二次函数的性质证明
,再利用二次函数的性质证明![]() ,则
,则![]() ,从而可得结论.
,从而可得结论.
试题解析:(Ⅰ)当![]() 时,
时, ![]() ,定义域为
,定义域为![]()
![]()
(i)![]()
![]()
所以切点坐标为![]() ,切线斜率为
,切线斜率为![]()
所以切线方程为![]()
(ii)令![]() ,
,![]()
所以![]() 在
在![]() 上单调递减,且
上单调递减,且![]()
所以当![]() 时,
时, ![]() 即
即![]()
所以当![]() 时,
时, ![]() 即
即![]()
综上所述, ![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(Ⅱ)方法一:
![]() ,即
,即![]()
设![]()
![]()
设![]()
![]()
所以![]() 在
在![]() 小于零恒成立
小于零恒成立
即![]() 在
在![]() 上单调递减
上单调递减
因为![]()
所以![]() ,
,![]()
所以在![]() 上必存在一个
上必存在一个![]() 使得
使得
![]()
即![]()
所以当![]() 时,
时, ![]() ,
, ![]() 单调递增
单调递增
当![]() 时,
时, ![]() ,
, ![]() 单调递减
单调递减
所以![]()
因为![]()
所以![]()
令![]() 得
得![]()
因为![]() ,所以
,所以![]() ,
,![]()
因为![]() ,所以
,所以![]() 恒成立
恒成立
即![]() 恒成立
恒成立
综上所述,当![]() 时,
时, ![]()
方法二:
![]() 定义域
定义域![]()
为了证明![]() ,即
,即![]()
只需证明![]() ,即
,即![]()
令![]()
则![]()
令![]() ,得
,得![]()
令![]() ,得
,得![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
所以![]()
即![]() ,则
,则![]()
令![]()
因为![]() ,所以
,所以![]()
所以![]() 恒成立
恒成立
即![]()
所以![]()
综上所述, ![]()
即当![]() 时,
时, ![]() .
.
【方法点晴】本题主要考查利用导数求曲线切线方程以及利用导数研究函数的单调性与极值,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.


科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数f(x)=2a2x-1-1的图象过定点(![]() ,-1);
,-1);
②已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x+1),若f(a)=-2则实数a=-1或2.
③若loga![]() >1,则a的取值范围是(
>1,则a的取值范围是(![]() ,1);
,1);
④若对于任意x∈R都f(x)=f(4-x)成立,则f(x)图象关于直线x=2对称;
⑤对于函数f(x)=lnx,其定义域内任意x1≠x2都满足f(![]() )≥
)≥![]()
其中所有正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+![]() .
.
(I)当a=![]() 时,求函数f(x)在x=0处的切线方程;
时,求函数f(x)在x=0处的切线方程;
(II)函数f(x)是否存在零点?若存在,求出零点的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的标准方程为
的标准方程为![]() ,
,![]() 为圆
为圆![]() 上的动点,直线
上的动点,直线![]() 的方程为
的方程为![]() ,动点
,动点![]() 在直线
在直线![]() 上.
上.
(1)求![]() 的最小值,并求此时点
的最小值,并求此时点![]() 的坐标;
的坐标;
(2)若![]() 点的坐标为
点的坐标为![]() ,过
,过![]() 作直线与圆
作直线与圆![]() 交于
交于![]() ,
,![]() 两点,当
两点,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某植物园准备建一个五边形区域的盆栽馆,三角形ABE为盆裁展示区,沿AB、AE修建观赏长廊,四边形BCDE是盆栽养护区,若BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=![]() 米。
米。
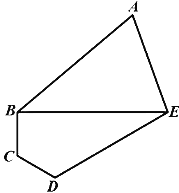
(1)求两区域边界BE的长度;
(2)若区域ABE为锐角三角形,求观赏长廊总长度AB+AE的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com