
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
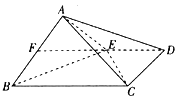
(Ⅰ)证明:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)见解析;
(II)![]()
【解析】
(Ⅰ)取BC的中点G,连接FG,EG,证明四边形EGCD为平行四边形,得EG∥平面ACD,再证明FG∥平面ACD,可得平面EFG∥平面ACD,从而得到EF∥平面ACD;
(Ⅱ)求解三角形证明BA⊥AE,取BE的中点H,连接AH,HC,证明AH⊥平面BCDE.以H为坐标原点,以过点H且平行于CD的直线为x轴,以过点H且平行于BC的直线为y轴,HA所在直线为z轴建立空间直角坐标系,求出平面ACD的一个法向量,再求出直线BC的方向向量,由两向量所成角的余弦值可得直线BC与平面ACD所成角的正弦值.
解:证明:(I)作![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
又![]() ,
,![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
故![]() ,则
,则![]() 平面
平面![]() ,
,
又![]()
![]() 为
为![]() 的中点,
的中点,![]() ,则
,则![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
(II)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,
又![]() ,
,![]() ,则
,则![]() ,
,
作![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,即
,即![]() ,
,
又![]() ,
,![]() 平面
平面![]() .
.
以![]() 为坐标原点,以过点
为坐标原点,以过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,以过点
轴,以过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,

可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则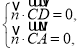 即
即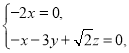
可得![]() ,
,
直线![]() 的方向向量
的方向向量![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则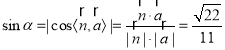 ,
,
综上,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,圆台O1O2的轴截面为等腰梯形A1A2B2B1,A1A2![]() B1B2,A1A2=2B1B2,A1B1=2,圆台O1O2的侧面积为6π.若点C,D分别为圆O1,O2上的动点且点C,D在平面A1A2B2B1的同侧.
B1B2,A1A2=2B1B2,A1B1=2,圆台O1O2的侧面积为6π.若点C,D分别为圆O1,O2上的动点且点C,D在平面A1A2B2B1的同侧.
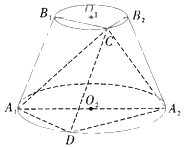
(1)求证:A1C⊥A2C;
(2)若∠B1B2C=60°,则当三棱锥C﹣A1DA2的体积取最大值时,求A1D与平面CA1A2所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节(每年农历五月初五),是中国传统节日,有吃粽子的习俗.某超市在端午节这一天,每售出![]() kg粽子获利润
kg粽子获利润![]() 元,未售出的粽子每
元,未售出的粽子每![]() kg亏损
kg亏损![]() 元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了
元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了![]() kg粽子.以
kg粽子.以![]() (单位:kg,
(单位:kg,![]() )表示今年的市场需求量,
)表示今年的市场需求量,![]() (单位:元)表示今年的利润.
(单位:元)表示今年的利润.
市场需求量(kg) |
|
|
|
|
|
频率 | 0.1 | 0.2 | 0.3 | 0.25 | 0.15 |
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据频率分布表估计今年利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于空间中的三条直线,有以下四个条件:①三条直线两两相交;②三条直线两两平行;③三条直线共点;④两直线相交,第三条平行于其中一条与另一条相交.其中使这三条直线共面的充分条件有______(填正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
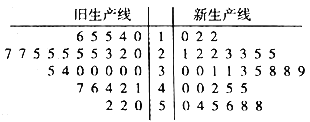
【题目】近几年,我国鲜切花产业得到了快速发展,相关部门制定了鲜切花产品行业等级标准,统一使用综合指标值![]() 进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
进行衡量,如下表所示.某花卉生产基地准备购进一套新型的生产线,现进行设备试用,分别从新旧两条生产线加工的产品中选取30个样品进行等级评定,整理成如图所示的茎叶图.
综合指标 |
|
|
|
质量等级 | 三级 | 二级 | 一级 |
(Ⅰ)根据茎叶图比较两条生产线加工的产品的综合指标值的平均值及分散程度(直接给出结论即可);
(Ⅱ)若从等级为三级的样品中随机选取3个进行生产流程调查,其中来自新型生产线的样品个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)根据该花卉生产基地的生产记录,原有生产线加工的产品的单件平均利润为4元,产品的销售率(某等级产品的销量与产量的比值)及产品售价如下表:
三级花 | 二级花 | 一级花 | |
销售率 |
|
|
|
单件售价 | 12元 | 16元 | 20元 |
预计该新型生产线加工的鲜切花单件产品的成本为10元,日产量3000件.因为鲜切花产品的保鲜特点,未售出的产品统一按原售价的50%全部处理完.如果仅从单件产品利润的角度考虑,该生产基地是否需要引进该新型生产线?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“金镶玉”是北京奥运会的奖牌设计所采用的式样,喻示中国传统文化中的“金玉良缘”,体现了中国人对奥林匹克精神的礼赞和对运动员的褒奖.它的设计方案,创意十分新颖,突破了以往任何一届奥运会奖牌设计单一材质的传统,又融入了典型的中国文化元素,是中国文化与体育精神完美结合的载体.现有一矩形玉片![]() ,
,![]() 为
为![]() 毫米,
毫米,![]() 为32毫米,
为32毫米,![]() 为
为![]() 的中点.现要开槽镶嵌金丝,将其加工为镶金工艺品,如图,金丝部分为优弧
的中点.现要开槽镶嵌金丝,将其加工为镶金工艺品,如图,金丝部分为优弧![]() 和线段
和线段![]() 其中优弧
其中优弧![]() 所在圆的圆心为
所在圆的圆心为![]() ,圆
,圆![]() 与矩形的边
与矩形的边![]() 分别相切于点
分别相切于点![]() 以及点
以及点![]() 在线段
在线段![]() 上(
上(![]() 在
在![]() 的左侧),
的左侧),![]() 分别于圆
分别于圆![]() 相切于点
相切于点![]() 且
且![]() .若优弧
.若优弧![]() 部分镶嵌的金丝每毫米造价为
部分镶嵌的金丝每毫米造价为![]() 元(
元(![]() ),线段
),线段![]() 部分镶嵌的金丝每毫米造价为
部分镶嵌的金丝每毫米造价为![]() 元.记锐角
元.记锐角![]() 镶嵌金丝的总造价为
镶嵌金丝的总造价为![]() 元.
元.
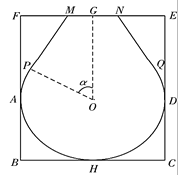
(1)试表示出关于![]() 的函数
的函数![]() 并写出
并写出![]() 的范围;
的范围;
(2)当镶嵌金丝的总造价最低时,求出四边形![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 有共同的焦点,且离心率为
有共同的焦点,且离心率为![]() ,设
,设![]() 分别是
分别是![]() 为椭圆的上下顶点
为椭圆的上下顶点
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,当弦
,当弦![]() 的中点
的中点![]() 落在四边形
落在四边形![]() 内(含边界)时,求直线
内(含边界)时,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com