
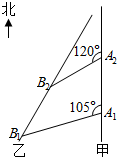
 如图所示,甲船以每小时30$\sqrt{2}$海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10$\sqrt{2}$海里.问:乙船每小时航行多少海里?
如图所示,甲船以每小时30$\sqrt{2}$海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10$\sqrt{2}$海里.问:乙船每小时航行多少海里? 分析 连接A1B2,则∴△A1A2B2是等边三角形,求出A1B2,在△A1B2B1中使用余弦定理求出B1B2的长,除以航行时间得出速度.
解答 解:如图,连接A1B2,由题意知,
A1B1=20,A2B2=10$\sqrt{2}$,A1A2=$\frac{20}{60}$×30$\sqrt{2}$=10$\sqrt{2}$(海里).
又∵∠B2A2A1=180°-120°=60°,
∴△A1A2B2是等边三角形,∴A1B2=10$\sqrt{2}$,∠B1A1B2=105-60°=45°.
在△A1B2B1中,由余弦定理得
B1B22=A1B12+A1B22-2A1B1•A1B2cos 45°
=202+(10$\sqrt{2}$)2-2×20×10$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=200,
∴B1B2=10$\sqrt{2}$(海里).
因此乙船的速度大小为$\frac{10\sqrt{2}}{20}$×60=30$\sqrt{2}$(海里/小时).
点评 本题考查了解三角形的实际应用,构造三角形寻找边角关系是解题关键.


科目:高中数学 来源: 题型:选择题
| A. | $y=cos(2x-\frac{1}{2})$ | B. | $y=cos(2x+\frac{1}{2})$ | C. | y=cos(2x-1) | D. | y=cos(2x+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,过曲线C:y=x3(x≥0)上点A1(2,8)作C的切线交x轴于点B1,过点B1作x轴的垂线交曲线C与点A2,过点A2作C的切线交x轴于点B2,再过点B2作x轴的垂线交曲线C与点A3,过点A3作C的切线交x轴于点B3,…、以此类推,得到一系列点:A1,B1,A2,B2,A3,B3,…记点An的横坐标为an.
如图,过曲线C:y=x3(x≥0)上点A1(2,8)作C的切线交x轴于点B1,过点B1作x轴的垂线交曲线C与点A2,过点A2作C的切线交x轴于点B2,再过点B2作x轴的垂线交曲线C与点A3,过点A3作C的切线交x轴于点B3,…、以此类推,得到一系列点:A1,B1,A2,B2,A3,B3,…记点An的横坐标为an.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com