
【题目】为了解学生对“两个一百年”奋斗目标、实现中华民族伟大复兴中国梦的“关注度”(单位:天),某中学团委在全校采用随机抽样的方法抽取了80名学生(其中男女人数各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月“关注度”分为6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
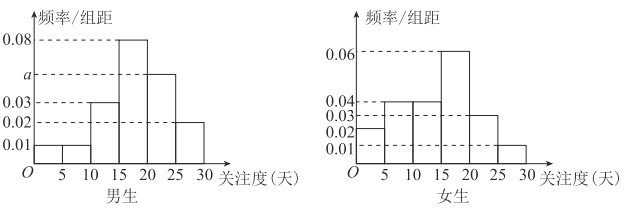
(1)求![]() 的值;
的值;
(2)求抽取的80名学生中月“关注度”不少于15天的人数;
(3)在抽取的80名学生中,从月“关注度”不少于25天的人中随机抽取2人,求至少抽取到1名女生的概率.
【答案】(1)![]() ;(2)50;(3)
;(2)50;(3)![]()
【解析】试题分析:(1)由频率分布直方图求得![]() 的值;(2)根据频率直方图求出女生、男生月上网次数不少于15次的频率,计算对应的频数,再求和;(3)利用列举法求基本事件数,计算对应的概率值即可.
的值;(2)根据频率直方图求出女生、男生月上网次数不少于15次的频率,计算对应的频数,再求和;(3)利用列举法求基本事件数,计算对应的概率值即可.
试题解析:
(1)由频率分布直方图,知![]() ,得
,得![]() .
.
(2)根据频率直方图求出女生、男生月上网次数不少于15次的频率,计算对应的频数,再求和;(3)记“在抽取的80名学生中,从月“关注度”不少于25天的人中随机抽取2人,至少抽到1名女生”为事件![]() ,在抽取的女生中,月“关注度”不少于25天的频率为
,在抽取的女生中,月“关注度”不少于25天的频率为![]() ,人数为
,人数为![]() 人,分别记为
人,分别记为![]() ,
, ![]() .在抽取的男生中,月“关注度”不少于25天的频率为
.在抽取的男生中,月“关注度”不少于25天的频率为![]() ,人数为
,人数为![]() 人,分别记为
人,分别记为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则在抽取的80名学生中,共有6人月“关注度”不少于25天,从中随机抽取2人,所有可能的结果为
,则在抽取的80名学生中,共有6人月“关注度”不少于25天,从中随机抽取2人,所有可能的结果为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共15种,
共15种,
而事件![]() 包含的结果有
包含的结果有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共9种,所以
共9种,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知f(x)=ax﹣2 , g(x)=loga|x|(a>0且a≠1),若f(4)g(﹣4)<0,则y=f(x),y=g(x)在同一坐标系内的大致图象是( )
A.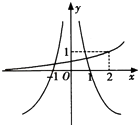
B.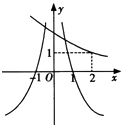
C.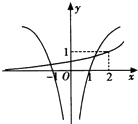
D.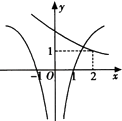
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,现要在一块半径为1m,圆心角为 ![]() 的扇形纸报AOB上剪出一个平行四边形MNPQ,使点P在弧AB上,点Q在OA上,点M、N在OB上,设∠BOP=θ,平行四边形MNPQ的面积为S.
的扇形纸报AOB上剪出一个平行四边形MNPQ,使点P在弧AB上,点Q在OA上,点M、N在OB上,设∠BOP=θ,平行四边形MNPQ的面积为S. 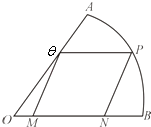
(1)求S关于θ的函数关系式;
(2)求S的最大值及相应的θ角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为2,线段D1B1上有两个动点E、F,且EF=1,则下列结论中错误的是( ) 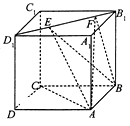
A.AC⊥BE
B.AA1∥平面BEF
C.三棱锥A﹣BEF的体积为定值
D.△AEF的面积和△BEF的面积相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x﹣a)2+(2﹣x+a)2 , x∈[﹣1,1].
(1)若设t=2x﹣2﹣x , 求出t的取值范围(只需直接写出结果,不需论证过程);并把f(x)表示为t的函数g(t);
(2)求f(x)的最小值;
(3)关于x的方程f(x)=2a2有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数为常数![]()
(1)当![]() 在
在![]() 处取得极值时,若关于x的方程
处取得极值时,若关于x的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数b的取值范围.
上恰有两个不相等的实数根,求实数b的取值范围.
(2)若对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com