
【题目】下列选项中说法正确的是( )
A.命题“p∨q为真”是命题“p∧q为真”的必要条件
B.向量 ![]() ,
, ![]() 满足
满足 ![]() ,则
,则 ![]() 与
与 ![]() 的夹角为锐角
的夹角为锐角
C.若am2≤bm2 , 则a≤b
D.“?x0∈R,x02﹣x0≤0”的否定是“?x∈R,x2﹣x≥0”
【答案】A
【解析】解:对于A,若p∨q为真命题,则p,q至少有一个为真命题,若p∧q为真命题,则p,q都为真命题,则“p∨q为真命题”是“p∧q为真命题”的必要不充分条件,正确; 对于B,根据向量数量积的定义,向量 ![]() ,
, ![]() 满足
满足 ![]() ,则
,则 ![]() 与
与 ![]() 的夹角为锐角或同向,故错;
的夹角为锐角或同向,故错;
对于C,如果m2=0时,am2≤bm2成立,a≤b不一定成立,故错;
对于D,“x0∈R,x02﹣x0≤0”的否定是“x∈R,x2﹣x>0”,故错.
故选:A.
A,根据p∨q、p∧q的真值表判定;
B,根据向量数量积的定义,向量 ![]() ,
, ![]() 满足
满足 ![]() ,则
,则 ![]() 与
与 ![]() 的夹角为锐角或同向;
的夹角为锐角或同向;
C,如果m2=0时,am2≤bm2成立,a≤b不一定成立;
D,“x0∈R,x02﹣x0≤0”的否定是“x∈R,x2﹣x>0”.


科目:高中数学 来源: 题型:
【题目】已知椭圆C1 , 抛物线C2焦点均在x轴上,C1的中心和C2顶点均为原点O,从每条曲线上各取两个点,将其坐标记录于表中,则C1的左焦点到C2的准线之间的距离为( )
x | 3 | ﹣2 | 4 |
|
y | -2 | 0 | ﹣4 |
|
A.![]() -1
-1
B.![]() -1
-1
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程选讲]在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C1的参数方程为 ![]() 为参数),曲线C2的极坐标方程为
为参数),曲线C2的极坐标方程为 ![]() .
.
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)设P为曲线C1上一点,Q曲线C2上一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1,在△ABC中,内角A,B,C的对边分别为a,b,c,且f(B)=1.
sinxcosx+2cos2x﹣1,在△ABC中,内角A,B,C的对边分别为a,b,c,且f(B)=1.
(1)求B;
(2)若 ![]()
![]() =3,求b的取值范围.
=3,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b∈R且a<b,若a3eb=b3ea , 则下列结论中一定正确的个数是( ) ①a+b>6;②ab<9;③a+2b>9;④a<3<b.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,3,则输出v的值为( ) 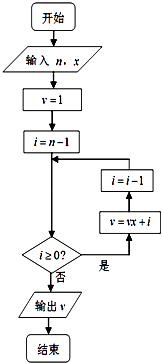
A.20
B.61
C.183
D.548
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为F1 , F2 , 上顶点为B,若△BF1F2的周长为6,且点F1到直线BF2的距离为b. (Ⅰ)求椭圆C的方程;
的左、右焦点分别为F1 , F2 , 上顶点为B,若△BF1F2的周长为6,且点F1到直线BF2的距离为b. (Ⅰ)求椭圆C的方程;
(Ⅱ)设A1 , A2是椭圆C长轴的两个端点,点P是椭圆C上不同于A1 , A2的任意一点,直线A1P交直线x=m于点M,若以MP为直径的圆过点A2 , 求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 若Sm﹣1=﹣4,Sm=0,Sm+2=14(m≥2,且m∈N*)
(Ⅰ)求m的值;
(Ⅱ)若数列{bn}满足 ![]() =log2bn(n∈N+),求数列{(an+6)bn}的前n项和.
=log2bn(n∈N+),求数列{(an+6)bn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com