
【题目】已知函数![]() 的最大值为
的最大值为![]() ,当
,当![]() 的定义域为
的定义域为![]() 时,
时,![]() 的值域为
的值域为![]() ,则正整数
,则正整数![]() 的最小值为( )
的最小值为( )
A.3B.4C.5D.6
【答案】D
【解析】
函数f(x)=asinωx+acosωx![]() asin(ωx
asin(ωx![]() ),由于函数f(x)的最大值为
),由于函数f(x)的最大值为![]() ,由
,由![]() a=2
a=2![]() ,解得a=±2.当f(x)的定义域为[1,2]时,f(x)的值域为[﹣2
,解得a=±2.当f(x)的定义域为[1,2]时,f(x)的值域为[﹣2![]() ,2
,2![]() ],包括最大值与最小值.若2﹣1
],包括最大值与最小值.若2﹣1![]() ,即ω≥2π,必定满足题意.若
,即ω≥2π,必定满足题意.若![]() 2﹣1
2﹣1![]() ,即π≤ω<2π,ω=4,5,6.通过验证即可得出.
,即π≤ω<2π,ω=4,5,6.通过验证即可得出.
函数f(x)=asinωx+acosωx![]() asin(ωx
asin(ωx![]() ),
),
由于函数f(x)的最大值为![]() ,∴
,∴![]() a=2
a=2![]() ,解得a=±2.
,解得a=±2.
当f(x)的定义域为[1,2]时,f(x)的值域为[﹣2![]() ,2
,2![]() ],包括最大值与最小值.
],包括最大值与最小值.
若2﹣1![]() ,即ω≥2π,必定满足题意.
,即ω≥2π,必定满足题意.
若![]() 2﹣1
2﹣1![]() ,即π≤ω<2π,ω=4,5,6.
,即π≤ω<2π,ω=4,5,6.
①取ω=6,f(x)=±2![]() sin(6x
sin(6x![]() ),6
),6![]() 6x
6x![]() 12
12![]() .
.
6x![]() 2π
2π![]() (>6
(>6![]() )时取最大值,6x
)时取最大值,6x![]() 2π
2π![]() (<12
(<12![]() )时取最小值.
)时取最小值.
②取ω=5,f(x)=±2![]() sin(5x
sin(5x![]() ),5
),5![]() 5x
5x![]() 10
10![]() .
.
5x![]() 2π
2π![]() (>5
(>5![]() )时取最大值,而5x
)时取最大值,而5x![]() 2π
2π![]() 10
10![]() ,因此不能取得最小值;同理可得ω=4也不合题意,
,因此不能取得最小值;同理可得ω=4也不合题意,
因此正整数ω的最小值为6.
故选:D.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数,
为参数,![]() ).
).
(1)若曲线![]() 与直线
与直线![]() 的一个交点纵坐标为
的一个交点纵坐标为![]() ,求
,求![]() 的值;
的值;
(2)若曲线![]() 上的点到直线
上的点到直线![]() 的最大距离为
的最大距离为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年6月14日,世界杯足球赛在俄罗斯拉开帷幕,世界杯给俄罗斯经济带来了一定的增长,某纪念商品店的销售人员为了统计世界杯足球赛期间商品的销售情况,随机抽查了该商品商店某天200名顾客的消费金额情况,得到如图频率分布表:将消费顾客超过4万卢布的顾客定义为”足球迷”,消费金额不超过4万卢布的顾客定义为“非足球迷”。
消费金额/万卢布 |
|
|
|
|
|
| 合计 |
顾客人数 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求这200名顾客消费金额的中位数与平均数(同一组中的消费金额用该组的中点值作代表;
(2)该纪念品商店的销售人员为了进一步了解这200名顾客喜欢纪念品的类型,采用分层抽样的方法从“非足球迷”,“足球迷”中选取5人,再从这5人中随机选取3人进行问卷调查,则选取的3人中“非足球迷”人数的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示1,已知四边形ABCD满足![]() ,
,![]() ,E是BC的中点.将
,E是BC的中点.将![]() 沿着AE翻折成
沿着AE翻折成![]() ,使平面
,使平面![]() 平面AECD,F为CD的中点,如图所示2.
平面AECD,F为CD的中点,如图所示2.
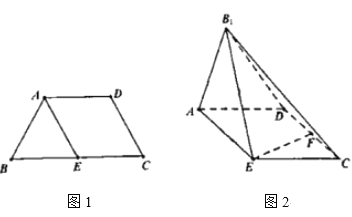
(1)求证:![]() 平面
平面![]() ;
;
(2)求AE到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆与双曲线![]() 有相同的焦点坐标,且点
有相同的焦点坐标,且点![]() 在椭圆上.
在椭圆上.
(1)求椭圆的标准方程;
(2)设A、B分别是椭圆的左、右顶点,动点M满足![]() ,垂足为B,连接AM交椭圆于点P(异于A),则是否存在定点T,使得以线段MP为直径的圆恒过直线BP与MT的交点Q,若存在,求出点T的坐标;若不存在,请说明理由.
,垂足为B,连接AM交椭圆于点P(异于A),则是否存在定点T,使得以线段MP为直径的圆恒过直线BP与MT的交点Q,若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.

(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)若数列![]() 是等差数列,且
是等差数列,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)若数列![]() 满足
满足![]()
![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
(3)设数列![]() 是等比数列,试探究当正实数
是等比数列,试探究当正实数![]() 满足什么条件时,数列
满足什么条件时,数列![]() 具有如下性质
具有如下性质![]() :对于任意的
:对于任意的![]()
![]() ,都存在
,都存在![]() 使得
使得![]() ,写出你的探求过程,并求出满足条件的正实数
,写出你的探求过程,并求出满足条件的正实数![]() 的集合.
的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com