
【题目】已知函数![]() .
.
(1)讨论f(x)的单调性;
(2)求函数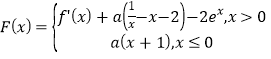 的零点个数.
的零点个数.
【答案】(1)见解析;(2)故a<0或a=e时,F(x)在y轴两侧各有1个零点,共2个零点,当a=0时,a(x+1)恒为0,F(x)有无数个零点.
【解析】
(1)对函数求导得到f′(x)=(x+1)(ex+a),分情况讨论导函数的正负,进而得到函数的单调性;(2)主要分析函数第一段的零点情况,令g(x)=xex﹣a(x>0),g′(x)=(x+1)ex>0,可得到函数g(x)单调增,通过讨论g(0)=﹣a和0的关系得到零点个数.
(1)f′(x)=(x+1)(ex+a),
a≥0时,x∈(﹣∞,﹣1)时,f′(x)<0,
x∈(﹣1,+∞)时,f′(x)>0,
故f(x)在(﹣∞,﹣1)递减,在(﹣1,+∞)递增,
a<0时,由f′(x)=0,解得:x=﹣1或x=ln(﹣a),
若a=﹣![]() ,则ln(﹣a)=﹣1,f′(x)≥0恒成立,
,则ln(﹣a)=﹣1,f′(x)≥0恒成立,
故f(x)在R递增,
若﹣![]() <a<0,则ln(﹣a)<﹣1,
<a<0,则ln(﹣a)<﹣1,
故x∈(﹣∞,ln(﹣a))∪(﹣1,+∞)时,f′(x)>0,
当x∈(ln(﹣a),﹣1)时,f′(x)<0,
故f(x)在(ln(﹣a),﹣1)递减,在(﹣∞,ln(﹣a)),(﹣1,+∞)递增;
若a<﹣![]() ,则ln(﹣a)>﹣1,
,则ln(﹣a)>﹣1,
当x∈(﹣∞,﹣1)∪(ln(﹣a),+∞)时,f′(x)>0,
当x∈(﹣1,ln(﹣a)时,f′(x)<0,
故f(x)在(﹣1,ln(﹣a))递减,在(﹣∞,﹣1),(ln(﹣a),+∞)递增,
综上,当a≥0时,f(x)在(﹣∞,﹣1)递减,在(﹣1,+∞)递增,
当﹣![]() <a<0时,f(x)在(ln(﹣a),﹣1)递减,在(﹣∞,ln(﹣a)),(﹣1,+∞)递增,
<a<0时,f(x)在(ln(﹣a),﹣1)递减,在(﹣∞,ln(﹣a)),(﹣1,+∞)递增,
当a=﹣![]() 时,f(x)在R递增,
时,f(x)在R递增,
当a<﹣![]() 时,f(x)在(﹣1,ln(﹣a))递减,在(﹣∞,﹣1),(ln(﹣a),+∞)递增;
时,f(x)在(﹣1,ln(﹣a))递减,在(﹣∞,﹣1),(ln(﹣a),+∞)递增;
(2)由已知得F(x)=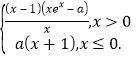 ,
,
令g(x)=xex﹣a(x>0),g′(x)=(x+1)ex>0,
故g(x)在(0,+∞)递增,
则g(x)>g(0)=﹣a,
故a<0或a=e时,F(x)在y轴两侧各有1个零点,共2个零点,
当a=0时,a(x+1)恒为0,F(x)有无数个零点.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=![]() ,PA=AD=2,AB=BC=1,点M、E分别是PA、PD的中点
,PA=AD=2,AB=BC=1,点M、E分别是PA、PD的中点
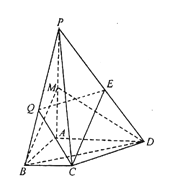
(1)求证:CE//平面BMD
(2)点Q为线段BP中点,求直线PA与平面CEQ所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国民法总则》(以下简称《民法总则》)自2017年10月1日起施行.作为民法典的开篇之作,《民法总则》与每个人的一生息息相关.某地区为了调研本地区人们对该法律的了解情况,随机抽取50人,他们的年龄都在区间![]() 上,年龄的频率分布及了解《民法总则》的入数如下表:
上,年龄的频率分布及了解《民法总则》的入数如下表:
年龄 |
|
|
|
|
|
|
频数 | 5 | 5 | 10 | 15 | 5 | 10 |
了解《民法总则》 | 1 | 2 | 8 | 12 | 4 | 5 |
(1)填写下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为以45岁为分界点对了解《民法总则》政策有差异;
的把握认为以45岁为分界点对了解《民法总则》政策有差异;
年龄低于45岁的人数 | 年龄不低于45岁的人数 | 合计 | |
了解 |
|
| |
不了解 |
|
| |
合计 |
(2)若对年龄在![]() ,
,![]() 的被调研人中各随机选取2人进行深入调研,记选中的4人中不了解《民法总则》的人数为
的被调研人中各随机选取2人进行深入调研,记选中的4人中不了解《民法总则》的人数为![]() ,求随机变量的分布列和数学期望.
,求随机变量的分布列和数学期望.
参考公式和数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.已知随机变量![]() ,若
,若![]() .则
.则![]()
B.已知分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观察值为
的观察值为![]() ,则当
,则当![]() 的值越大时,“
的值越大时,“![]() 与
与![]() 有关”的可信度越小.
有关”的可信度越小.
C.在线性回归模型中,计算其相关指数![]() ,则可以理解为:解析变量对预报变量的贡献率约为
,则可以理解为:解析变量对预报变量的贡献率约为![]()
D.若对于变量![]() 与
与![]() 的
的![]() 组统计数据的线性回归模型中,相关指数
组统计数据的线性回归模型中,相关指数![]() .又知残差平方和为
.又知残差平方和为![]() .那么
.那么![]() .(注意:
.(注意: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《五曹算经》是我国南北朝时期数学家甄鸾为各级政府的行政人员编撰的一部实用算术书.其第四卷第九题如下:“今有平地聚粟,下周三丈高四尺,问粟几何?”其意思为“场院内有圆锥形稻谷堆,底面周长3丈,高4尺,那么这堆稻谷有多少斛?”已知1丈等于10尺,1斜稻谷的体积约为1.62立方尺,圆周率约为3,估算出堆放的稻谷约有( )
A.57.08斜B.171.24斛C.61.73斛D.185.19斛
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的有( )个
(1). 残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高.
(2). 回归直线一定过样本中心![]() 。
。
(3). 两个模型中残差平方和越小的模型拟合的效果越好。
(4) .甲、乙两个模型的![]() 分别约为0.88和0.80,则模型乙的拟合效果更好.
分别约为0.88和0.80,则模型乙的拟合效果更好.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com