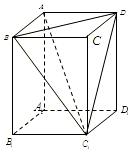
已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,高AA1=2,求:
(1)直线AC1与平面AA1B1B所成角的大小;
(2)二面角B-AC1-D的大小;
(3)四面体ABDC1的体积.
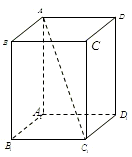
解:(1)连接AB
1,∵正四棱柱ABCD-A
1B
1C
1D
1,
∴B
1C
1⊥平面ABB
1A
1,AB
1是AC
1在平面AA
1B
1B上的射影,
∴∠C
1AB
1就是AC
1与平面AA
1B
1B所成的角,
在△C
1AB
1中,
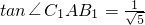
,
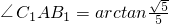
,
∴直线AC
1与平面AA
1B
1B所成的角为

.
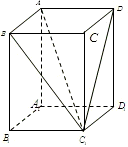
(2)过B作BE⊥AC,垂足为E,连接ED,
∵△ABC
1≌△ADC
1,∴∠BAC
1=∠DAC
1,
∵AB=AD,∠BAC
1=∠DAC
1,AE=AE
∴△ABE≌△ADE,
∴
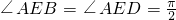
∴∠BED是二面角B-AC
1-D的平面角,
在△BED中,
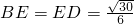
,
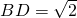
,
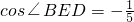
,
∴
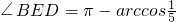
∴二面角B-AC
1-D的大小为
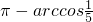
.
(3)
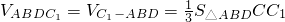
=

.
分析:(1)连接AB
1,由正四棱柱ABCD-A
1B
1C
1D
1,知B
1C
1⊥平面ABB
1A
1,AB
1是AC
1在平面AA
1B
1B上的射影,故∠C
1AB
1就是AC
1与平面AA
1B
1B所成的角,由此能求出直线AC
1与平面AA
1B
1B所成的角.
(2)过B作BE⊥AC,垂足为E,连接ED,由△ABC
1≌△ADC
1,知∠BAC
1=∠DAC
1,由AB=AD,∠BAC
1=∠DAC
1,AE=AE,知△ABE≌△ADE,由此能求出二面角B-AC
1-D的大小.
(3)
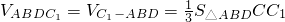
,由此能求出四面体ABDC
1的体积.
点评:本题考查直线与平面所成角的大小的求法,考查二面角面积的求法,考查四面体体积的求法,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

 解:(1)连接AB1,∵正四棱柱ABCD-A1B1C1D1,
解:(1)连接AB1,∵正四棱柱ABCD-A1B1C1D1,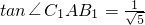 ,
,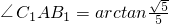 ,
, .
.
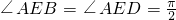
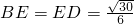 ,
,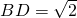 ,
,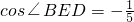 ,
,
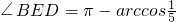
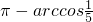 .
.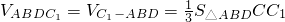 =
= .
.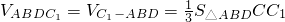 ,由此能求出四面体ABDC1的体积.
,由此能求出四面体ABDC1的体积.

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案 如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,
如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1, 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.