
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:| 2x-$\frac{π}{3}$ | -$\frac{4π}{3}$ | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{2π}{3}$ |
| x | -$\frac{π}{2}$ | -$\frac{π}{3}$ | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{π}{2}$ |
| f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过E点做EF⊥PB交PB于点F.求证:
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过E点做EF⊥PB交PB于点F.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4≤a≤9 | B. | a≤-4或a≥9 | C. | -9≤a≤4 | D. | a≤-9或a≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
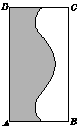 如图,面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD中随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为350个,试估计阴影部分的面积为( )
如图,面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD中随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为350个,试估计阴影部分的面积为( )| A. | 1.4 | B. | 1.6 | C. | 2.6 | D. | 2.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com