
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)若a=1,求曲线f(x)在点(e,f(e))处的切线方程;
(Ⅱ)求f(x)的极值;
(Ⅲ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围.
【答案】(1) x+e2y-3e=0 (2) a≥1.
【解析】试题分析:(Ⅰ)由切点坐标,根据导数的几何意义,求出该点的导数值,即得曲线在此点处的切线的斜率,然后用点斜式写出切线方程即可;(Ⅱ)求出函数![]() 的导函数,令导数大于0解出增区间,令导数小于0,解出函数的减区间,然后由极值判断规则确定出极值即可;
的导函数,令导数大于0解出增区间,令导数小于0,解出函数的减区间,然后由极值判断规则确定出极值即可;
(Ⅲ)若函数![]() 的图象与函数
的图象与函数![]() 的图象在区间
的图象在区间![]() 上有公共点,即在区间
上有公共点,即在区间![]() 上,函数
上,函数![]() 存在自变量取某个值时,函数值等于1,故问题可以转化为求出函数
存在自变量取某个值时,函数值等于1,故问题可以转化为求出函数![]() 最值,保证函数的最大值大于等于1,最小值小于等于1,即可得到关于参数
最值,保证函数的最大值大于等于1,最小值小于等于1,即可得到关于参数![]() 的不等式,解之即得.
的不等式,解之即得.
试题解析:(Ⅰ) a=1, ![]() 且
且![]()
又∵![]()
∴![]()
∴f(x)在点(e,f(e))处的切线方程为: ![]() ,即x+e2y-3e=0.
,即x+e2y-3e=0.
(Ⅱ)f(x)的定义域为(0,+∞), ![]()
令f′(x)=0得x=e1-a.
当x∈(0,e1-a)时,f′(x)>0,f(x)是增函数;
当x∈(e1-a,+∞)时,f′(x)<0,f(x)是减函数;
f(x)在x=e1-a处取得极大值,
即f(x)极大值=f(e1-a)=ea-1
(Ⅲ)(i)当e1-a<e2,即a>-1时,
由(Ⅱ)知f(x)在(0,e1-a)上是增函数,
在(e1-a,e2]上是减函数,
当x=e1-a时,f(x)取得最大值,
即f(x)max=ea-1.
又当x=e-a时,f(x)=0,
当x∈(0,e-a]时,f(x)<0,
当x∈(e-a,e2]时,f(x)∈(0,ea-1],
所以,f(x)的图象与g(x)=1的图象在(0,e2]上有公共点,
等价于ea-1≥1,解得a≥1,
又因为a>-1,所以a≥1.
(ii)当e1-a≥e2,即a≤-1时,f(x)在(0,e2]上是增函数,
f(x)在(0,e2]上的最大值为f(e2)=![]() ,
,
原问题等价于![]() ≥1,解得a≥e2-2,
≥1,解得a≥e2-2,
又a≤-1 无解
综上,a的取值范围是a≥1.


科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为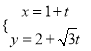 (t为参数).
(t为参数).
(1)写出直线l的普通方程与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换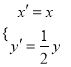 得到曲线,设M(x,y)为
得到曲线,设M(x,y)为![]() 上任意一点,求
上任意一点,求![]() 的最小值,并求相应的点M的坐标.
的最小值,并求相应的点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856288)
设函数f(x)=aln x-x,g(x)=aex-x,其中a为正实数.
(Ⅰ)若f(x)在(1,+∞)上是单调减函数,且g(x)在(2,+∞)上有最小值,求a的取值范围;
(Ⅱ)若函数f(x)与g(x)都没有零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x+1|﹣|2x﹣3|,g(x)=|x+1|+|x﹣a|.
(l)求f(x)≥1的解集;
(2)若对任意的t∈R,s∈R,都有g(s)≥f(t).求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)选修4-2:矩阵与变换
求矩阵![]() 的特征值和特征向量.
的特征值和特征向量.
(2)选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的方程为
的方程为![]() ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,圆
轴的正半轴建立平面直角坐标系,圆![]() 的参数方程
的参数方程![]() (
(![]() 是参数),若圆
是参数),若圆![]() 与圆
与圆![]() 相切,求实数
相切,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856295)德国大数学家高斯年少成名,被誉为数学王子.19岁的高斯得到了一个数学史上非常重要的结论,就是《正十七边形尺规作图之理论与方法》, 在其年幼时,对1+2+3+…+100的求和运算中,提出了倒序相加法的原理,该原理基于所给数据前后对应项的和呈现一定的规律生成,因此,此方法也被称为高斯算法.现有函数f(x)=![]() ,则f(1)+f(2)+…+f(m+2017)等于( )
,则f(1)+f(2)+…+f(m+2017)等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856331)
甲、乙两家快餐店对某日7个时段的光顾的客人人数进行统计并绘制茎叶图如下图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
(Ⅰ)求a,b的值,并计算乙数据的方差;
(Ⅱ)现从乙数据中不大于16的数据中随机抽取两个,求至少有一个数据小于10的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的五面体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 是正方形,二面角
是正方形,二面角![]() 的大小为
的大小为![]() .
.

(1)在线段![]() 上找出一点
上找出一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com