
分析 (1)求出圆的半径,即可求圆N的方程;
(2)根据题意得到直线l斜率存在,设为k,表示出直线l方程,利用点到直线的距离公式表示出圆心到直线l的距离d,根据r与弦长,利用垂径定理及勾股定理列出关于k的方程,求出方程的解得到k的值即可.
解答 解:(1)由题意,圆心到直线的距离为3-1=2,
∵圆N被直线x=1截得的弦长为2$\sqrt{5}$,
∴圆的半径r=$\sqrt{5+4}$=3,
∴圆N的方程为(x-3)2+(y-4)2=9;
(2)设直线l方程为y-6=k(x-3),即kx-y-3k+6=0,
∵圆心(3,4)到直线l的距离d=$\frac{2}{\sqrt{1+{k}^{2}}}$,r=3,弦长为4$\sqrt{2}$,
∴4$\sqrt{2}$=2$\sqrt{9-{d}^{2}}$,化简得1+k2=4,解得:k=±$\sqrt{3}$.
点评 此题考查了直线与圆相交的性质,涉及的知识有:点到直线的距离公式,圆的标准方程,垂径定理,以及勾股定理,熟练掌握公式及定理是解本题的关键.


 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
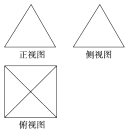 一个几何体的三视图如图所示,正视图和侧视图都是等边三角形,且该几何体的四个点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(2,0,0),(0,2,0),则第五个顶点的坐标可能为( )
一个几何体的三视图如图所示,正视图和侧视图都是等边三角形,且该几何体的四个点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(2,0,0),(0,2,0),则第五个顶点的坐标可能为( )| A. | (1,1,1) | B. | (1,1,$\sqrt{2}$) | C. | (1,1,$\sqrt{3}$) | D. | (2,2,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 甲、乙两组各有三名同学,她们在一次测试中的成绩的茎叶图如图所示,如果分别从甲、乙两组中随机选取一名同学,则这两名同学的成绩之差的绝对值不超过3的概率是$\frac{8}{9}$.
甲、乙两组各有三名同学,她们在一次测试中的成绩的茎叶图如图所示,如果分别从甲、乙两组中随机选取一名同学,则这两名同学的成绩之差的绝对值不超过3的概率是$\frac{8}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p为:?x∈(1,+∞),2x-1-1≤0 | B. | ¬p为:?x∈(1,+∞),2x-1-1<0 | ||
| C. | ¬p为:?x∈(-∞,1],2x-1-1>0 | D. | ¬p是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥l,则α∥β | B. | 若α⊥β,则m∥l | C. | 若m⊥l,则α∥β | D. | 若α∥β,则m⊥l |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com