
【题目】函数f(x)=2sin(2x+ ![]() ),g(x)=mcos(2x﹣
),g(x)=mcos(2x﹣ ![]() )﹣2m+3(m>0),若对任意x1∈[0,
)﹣2m+3(m>0),若对任意x1∈[0, ![]() ],存在x2∈[0,
],存在x2∈[0, ![]() ],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
科目:高中数学 来源: 题型:
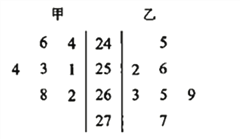
【题目】双十一网购狂欢,快递业务量猛增.甲、乙两位快递员![]() 月
月![]() 日到
日到![]() 日每天送件数量的茎叶图如图所示.
日每天送件数量的茎叶图如图所示.
(Ⅰ)根据茎叶图判断哪个快递员的平均送件数量较多(写出结论即可);
(Ⅱ)求甲送件数量的平均数;
(Ⅲ)从乙送件数量中随机抽取![]() 个,求至少有一个送件数量超过甲的平均送件数量的概率.
个,求至少有一个送件数量超过甲的平均送件数量的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)的图象关于点(﹣ ![]() ,0)成中心对称,且对任意的实数x都有
,0)成中心对称,且对任意的实数x都有 ![]() ,f(﹣1)=1,f(0)=﹣2,则f(1)+f(2)+…+f(2 017)=( )
,f(﹣1)=1,f(0)=﹣2,则f(1)+f(2)+…+f(2 017)=( )
A.0
B.﹣2
C.1
D.﹣4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在其定义区间[a,b]上满足①f(x)>0;②f′(x)<0;③对任意的x1 , x2∈[a,b],式子 ![]() ≤
≤ ![]() 恒成立.记S1=
恒成立.记S1= ![]() f(x)dx,S2=
f(x)dx,S2= ![]() (b﹣a),S3=f(b)(b﹣a),则S1 , S2 , S3的大小关系为 . (按由小到大的顺序)
(b﹣a),S3=f(b)(b﹣a),则S1 , S2 , S3的大小关系为 . (按由小到大的顺序)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲乙丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是( )
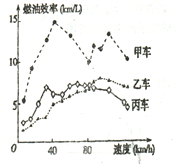
A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比乙车更省油.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .任取t∈R,若函数f(x)在区间[t,t+1]上的最大值为M(t),最小值为m(t),记g(t)=M(t)﹣m(t).
.任取t∈R,若函数f(x)在区间[t,t+1]上的最大值为M(t),最小值为m(t),记g(t)=M(t)﹣m(t).
(1)求函数f(x)的最小正周期及对称轴方程;
(2)当t∈[﹣2,0]时,求函数g(t)的解析式;
(3)设函数h(x)=2|x﹣k|,H(x)=x|x﹣k|+2k﹣8,其中实数k为参数,且满足关于t的不等式 ![]() 有解,若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得h(x2)=H(x1)成立,求实数k的取值范围.
有解,若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得h(x2)=H(x1)成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
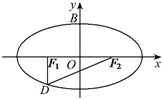
【题目】如图,设椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,点
,点![]() 在椭圆上,
在椭圆上, ![]() ,
, ![]() ,
, ![]() 的面积为
的面积为![]() .
.
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)是否存在圆心在![]() 轴上的圆,使圆在
轴上的圆,使圆在![]() 轴的上方与椭圆
轴的上方与椭圆
有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com