
【题目】如图,四边形ABCD为正方形,![]() ,且
,且![]() ,
,![]() 平面BCE.
平面BCE.
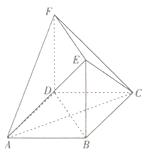
(1)证明:平面![]() 平面BDFE;
平面BDFE;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)先推导出![]() ,
,![]() ,证得
,证得![]() 平面ABCD,进而得到
平面ABCD,进而得到![]() ,由此能力证明
,由此能力证明![]() 平面BDFE,从而得到平面
平面BDFE,从而得到平面![]() 平面BDFE;
平面BDFE;
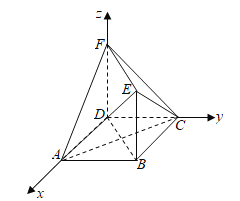
(2)以D为坐标原点建立如图所示的空间直角坐标系![]() ,分别求得平面
,分别求得平面![]() 的法向量,结合向量的夹角公式,即可求解.
的法向量,结合向量的夹角公式,即可求解.
(1)由题意,因为四边形ABCD为正方形,![]() .
.
![]() ,
,![]() ,
,![]() .
.
又![]() 平面BCE,
平面BCE,![]() .
.
![]() ,
,![]() 平面ABCD,
平面ABCD,![]() .
.
又![]() ,
,![]() 平面BDFE,
平面BDFE,
![]() 平面AEC,
平面AEC,![]() 平面
平面![]() 平面BDFE.
平面BDFE.
(2)![]() 平面ABCD,
平面ABCD,![]() ,所以
,所以![]() 平面ABCD,
平面ABCD,
以D为坐标原点建立如图所示的空间直角坐标系![]() ,令
,令![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设平面AFC的法向量为![]() ,则
,则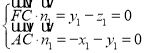 ,
,
令![]() ,则
,则![]() ,所以
,所以![]() ,
,
设平面EFC的法向量为![]() ,则
,则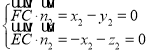 ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
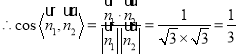 .
.
因为二面角![]() 为锐角,所以二面角
为锐角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 与
与![]() 轴正半轴的交点,
轴正半轴的交点,![]() 上是否存在两点
上是否存在两点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,请说明满足条件的
为直角顶点的等腰直角三角形?若存在,请说明满足条件的![]() 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次![]() 公里的自行车个人赛中,25名参赛选手的成绩(单位:分钟)的茎叶图如图所示:
公里的自行车个人赛中,25名参赛选手的成绩(单位:分钟)的茎叶图如图所示:

(1)现将参赛选手按成绩由好到差编为1~25号,再用系统抽样方法从中选取5人,已知选手甲的成绩为85分钟,若甲被选取,求被选取的其余4名选手的成绩的平均数;
(2)若从总体中选取一个样本,使得该样本的平均水平与总体相同,且样本的方差不大于7,则称选取的样本具有集中代表性,试从总体(25名参赛选手的成绩)选取一个具有集中代表性且样本容量为5的样本,并求该样本的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂有![]() 台大型机器,在
台大型机器,在![]() 个月中,
个月中,![]() 台机器至多出现
台机器至多出现![]() 次故障,且每台机器是否出现故障是相互独立的,出现故障时需
次故障,且每台机器是否出现故障是相互独立的,出现故障时需![]() 名工人进行维修.每台机器出现故障的概率为
名工人进行维修.每台机器出现故障的概率为![]() .已知
.已知![]() 名工人每月只有维修
名工人每月只有维修![]() 台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得
台机器的能力,每台机器不出现故障或出现故障时有工人维修,就能使该厂获得![]() 万元的利润,否则将亏损
万元的利润,否则将亏损![]() 万元.该工厂每月需支付给每名维修工人
万元.该工厂每月需支付给每名维修工人![]() 万元的工资.
万元的工资.
(1)若每台机器在当月不出现故障或出现故障时有工人进行维修,则称工厂能正常运行.若该厂只有![]() 名维修工人,求工厂每月能正常运行的概率;
名维修工人,求工厂每月能正常运行的概率;
(2)已知该厂现有![]() 名维修工人.
名维修工人.
(ⅰ)记该厂每月获利为![]() 万元,求
万元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(ⅱ)以工厂每月获利的数学期望为决策依据,试问该厂是否应再招聘![]() 名维修工人?
名维修工人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com