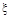练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    掷两颗骰子，所得点数之和为，那么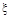=4表示的随机试验结果是（  ）
    A．一颗是3点，一颗是1点B．两颗都是2点
    C．两颗都是4点D．一颗是3点，一颗是1点或两颗都是2点
    D

    试题分析：∵=4表示两个骰子之和为4，有（3,1），（1,3），（2,2），即=4表示的随机试验结果是一颗是3点，一颗是1点或两颗都是2点，故选D
    点评：熟练掌握随机变量的概念是解决此类问题的关键，属基础题
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    (文)在某次普通测试中，为测试汉字发音水平，设置了10张卡片，每张卡片上印有一个汉字的拼音，其中恰有3张卡片上的拼音带有后鼻音“g”.
    （I）现对三位被测试者先后进行测试，第一位被测试者从这10张卡片中随机抽取1张。测试后放回，余下2位的测试，也按同样的方法进行，求这三位被测试者抽取的卡片上，拼音都带有后鼻音“g”的概率：
    （Ⅱ）若某位被测试者从这10张卡片中一次随机抽取3张，求这3张卡片上，拼音带有后鼻音“g”的卡片不少于2张的概率

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

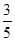    已知一个射手每次击中目标的概率为p＝，他在4次射击中，命中两次的概率为________，刚好在第二、第三两次击中目标的概率为________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

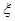    甲与乙两人掷硬币，甲用一枚硬币掷3次，记正面朝上的次数为；乙用这枚硬币掷2次，记正面朝上的次数为。
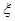    （1）分别求与的期望；
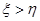    （2）规定：若，则甲获胜；若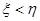，则乙获胜，分别求出甲和乙获胜的概率.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

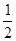    高三年级有3名男生和1名女生为了报某所大学，事先进行了多方详细咨询，并根据自己的高考成绩情况，最终估计这3名男生报此所大学的概率都是，这1名女生报此所大学的概率是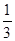．且这4人报此所大学互不影响。
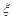    （Ⅰ）求上述4名学生中报这所大学的人数中男生和女生人数相等的概率；
    （Ⅱ）在报考某所大学的上述4名学生中，记为报这所大学的男生和女生人数的和，试求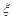的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

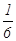    为了防止受到核污染的产品影响我国民众的身体健康，要求产品进入市场前必须进行两轮核放射检测，只有两轮都合格才能进行销售。已知某产品第一轮检测不合格的概率为，第二轮检测不合格的概率为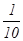，两轮检测是否合格相互没有影响。
    （1）求该产品不能销售的概率
    （2）如果产品可以销售，则每件产品可获利40元；如果产品不能销售，则每件产品亏损80元（即获利-80元）。已知一箱中有4件产品，记可销售的产品数为X，求X的分布列，并求一箱产品获利的均值。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某种种子每粒发芽的概率都为0.9，现播种了1 000粒，对于没有发芽的种子，每粒需再补种2粒，补种的种子数记为X，则X的均值为(　　)
    A．100B．200C．300D．400

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    5名工人独立地工作，假定每名工人在1小时内平均12分钟需要电力（即任一时刻需要电力的概率为12/60）
    （1）设X为某一时刻需要电力的工人数，求 X的分布列及期望；
    （2）如果同一时刻最多能提供3名工人需要的电力，求电力超负荷的概率，并解释实际意义．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    从某批产品中，有放回地抽取产品2次，每次随机抽取1件，假设事件A：“取出的2件产品中至多有1件是二等品”的概率为0.84．
    （Ⅰ）求事件“从该批产品中任取1件产品，取到的是二等品”的概率p；
    （Ⅱ）若从20件该产品中任意抽取3件，求事件B：“取出的3件产品中至少有一件二等品”的概率．

    查看答案和解析>>

    同步练习册答案