
【题目】在△AOB中,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,△AOC为钝角三角形的概率是( )
A.0.2
B.0.4
C.0.6
D.0.8
科目:高中数学 来源: 题型:
【题目】在一次数学考试中,第22题和第23题为选做题,规定每位考生必须且只须在其中选做一题,现有甲、乙、丙、丁4名考生参加考试,其中甲、乙选做第22题的概率均为![]() ,丙、丁选做第22题的概率均为
,丙、丁选做第22题的概率均为![]() .
.
(Ⅰ)求在甲选做第22题的条件下,恰有两名考生选做同一道题的概率;
(Ⅱ)设这4名考生中选做第22题的学生个数为X,求X的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限![]() (单位:年,
(单位:年, ![]() )和所支出的维护费用
)和所支出的维护费用![]() (单位:万元)厂家提供的统计资料如下:
(单位:万元)厂家提供的统计资料如下:

(1)请根据以上数据,用最小二乘法原理求出维护费用![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若规定当维护费用![]() 超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
参考公式:最小二乘估计线性回归方程![]() 中系数计算公式:
中系数计算公式:
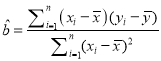 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,直线
轴非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程及直线
的极坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于 . 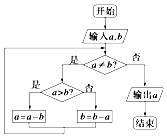
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】静宁县是甘肃苹果栽培第一大县,中国著名优质苹果基地和重要苹果出口基地.静宁县海拔高、光照充足、昼夜温差大、环境无污染,适合种植苹果.“静宁苹果”以色泽鲜艳、质细汁多,酸甜适度,口感脆甜、货架期长、极耐储藏和长途运输而著名.为检测一批静宁苹果,随机抽取50个,其重量(单位:克)的频数分布表如下:
分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
频数(个) | 5 | 10 | 20 | 15 |
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十三届全运会将于2017年9月在天津举行,组委会在2017年1月对参加接待服务的10名宾馆经理进行为期半月的培训,培训结束,组织了一次培训结业测试,10人考试成绩如下(满分100分):
75 84 65 90 88 95 78 85 98 82
(Ⅰ)以成绩的十位为茎、个位为叶作出本次结业成绩的茎叶图,并计算平均成绩与成绩的中位数 ;
(Ⅱ)从本次成绩在85分以上(含85分)的学员中任选2人,2人成绩都在90分以上(含90分)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com