
分析 (1)通过若$x≤-\frac{1}{2}$,若$-\frac{1}{2}<x<\frac{2}{3}$,若$x≥\frac{2}{3}$,化简不等式求出解集,利用已知条件,求解a,b.
(2)由(1)知a=1,b=2,求出绝对值的最值,得到m2-3m+5≤3,然后求解实数m的最大值.
解答 解:(1)若$x≤-\frac{1}{2}$,原不等式可化为-2x-1-3x+2≤5,解得$x≥-\frac{4}{5}$,即$-\frac{4}{5}≤x≤-\frac{1}{2}$;
若$-\frac{1}{2}<x<\frac{2}{3}$,原不等式可化为2x+1-3x+2≤5,解得x≥-2,即$-\frac{1}{2}<x<\frac{2}{3}$;
若$x≥\frac{2}{3}$,原不等式可化为2x+1+3x-2≤5,解得$x≤\frac{6}{5}$,即$\frac{2}{3}≤x≤\frac{6}{5}$;
综上所述,不等式|2x+1|+|3x-2|≤5的解集为$[-\frac{4}{5},\frac{6}{5}]$,所以a=1,b=2.
(2)由(1)知a=1,b=2,所以|x-a|+|x+b|=|x-1|+|x+2|≥|x-1-x-2|=3,
故m2-3m+5≤3,m2-3m+2≤0,所以1≤m≤2,即实数m的最大值为2.
点评 本题考查函数恒成立,绝对值不等式的解法,考查分类讨论思想的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (3,4) | C. | (-2,0) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
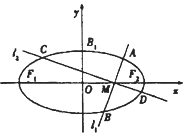 设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,点B1为其短轴的一个端点,满足$|{\overrightarrow{{B_1}{F_1}}+\overrightarrow{{B_1}{F_2}}}|=2|{\overrightarrow{{B_1}{F_1}}}|+|{\overrightarrow{{B_1}{F_2}}}|=2,\overrightarrow{{B_1}{F_1}}•\overrightarrow{{B_1}{F_2}}$=-2.
设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,点B1为其短轴的一个端点,满足$|{\overrightarrow{{B_1}{F_1}}+\overrightarrow{{B_1}{F_2}}}|=2|{\overrightarrow{{B_1}{F_1}}}|+|{\overrightarrow{{B_1}{F_2}}}|=2,\overrightarrow{{B_1}{F_1}}•\overrightarrow{{B_1}{F_2}}$=-2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | y=2|cosx| | C. | $y=cos\frac{x}{2}$ | D. | y=tan(-x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com