
【题目】平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为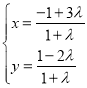 (
(![]() 为参数,且
为参数,且![]() ).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点P的极坐标为![]() ,Q为曲线
,Q为曲线![]() 上的动点,求
上的动点,求![]() 的中点M到曲线
的中点M到曲线![]() 的距离的最大值.
的距离的最大值.
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】一胸针图样由等腰三角形![]() 及圆心
及圆心![]() 在中轴线上的圆弧
在中轴线上的圆弧![]() 构成,已知
构成,已知![]() ,
,![]() .为了增加胸针的美观程度,设计师准备焊接三条金丝线
.为了增加胸针的美观程度,设计师准备焊接三条金丝线![]() 且
且![]() 长度不小于
长度不小于![]() 长度,设
长度,设![]() .
.

(1)试求出金丝线的总长度![]() ,并求出
,并求出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,金丝线的总长度
为何值时,金丝线的总长度![]() 最小,并求出
最小,并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中医药研究所研制出一种新型抗癌药物,服用后需要检验血液是否为阳性,现有![]() 份血液样本每个样本取到的可能性均等,有以下两种检验方式:(1)逐份检验,则需要检验
份血液样本每个样本取到的可能性均等,有以下两种检验方式:(1)逐份检验,则需要检验![]() 次;(2)混合检验,将其中
次;(2)混合检验,将其中![]() 份血液样本分别取样混合在一起检验,若结果为阴性,则这
份血液样本分别取样混合在一起检验,若结果为阴性,则这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只需检验一次就够了;若检验结果为阳性,为了明确这
份血液样本只需检验一次就够了;若检验结果为阳性,为了明确这![]() 份血液究竟哪份为阳性,就需要对这
份血液究竟哪份为阳性,就需要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次假设在接受检验的血液样本中,每份样本的检验结果总阳性还是阴性都是相互独立的,且每份样本是阳性的概率为
次假设在接受检验的血液样本中,每份样本的检验结果总阳性还是阴性都是相互独立的,且每份样本是阳性的概率为![]() .
.
(1)假设有6份血液样本,其中只有两份样本为阳性,若采取遂份检验的方式,求恰好经过两次检验就能把阳性样本全部检验出来的概率.
(2)现取其中的![]() 份血液样本,记采用逐份检验的方式,样本需要检验的次数为
份血液样本,记采用逐份检验的方式,样本需要检验的次数为![]() ;采用混合检验的方式,样本简要检验的总次数为
;采用混合检验的方式,样本简要检验的总次数为![]() ;
;
(ⅰ)若![]() ,试运用概率与统计的知识,求
,试运用概率与统计的知识,求![]() 关于
关于![]() 的函数关系
的函数关系![]() ,
,
(ⅱ)若![]() ,采用混合检验的方式需要检验的总次数的期望比逐份检验的总次数的期望少,求
,采用混合检验的方式需要检验的总次数的期望比逐份检验的总次数的期望少,求![]() 的最大值(
的最大值(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题.
C.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
D.若“p或q”为真命题,则p,q至少有一个为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过F的直线与抛物线交于A,B两点,点O为坐标原点,则下列命题中正确的个数为( )
的焦点为F,过F的直线与抛物线交于A,B两点,点O为坐标原点,则下列命题中正确的个数为( )
①![]() 面积的最小值为4;
面积的最小值为4;
②以![]() 为直径的圆与x轴相切;
为直径的圆与x轴相切;
③记![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④过焦点F作y轴的垂线与直线![]() ,
,![]() 分别交于点M,N,则以
分别交于点M,N,则以![]() 为直径的圆恒过定点.
为直径的圆恒过定点.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为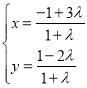 (
(![]() 为参数,且
为参数,且![]() ).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点P的极坐标为![]() ,Q为曲线
,Q为曲线![]() 上的动点,求
上的动点,求![]() 的中点M到曲线
的中点M到曲线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节期间,武汉市爆发了新型冠状病毒肺炎疫情,在党中央的坚强领导下,全国人民团结一心,众志成城,共同抗击疫情.某中学寒假开学后,为了普及传染病知识,增强学生的防范意识,提高自身保护能力,校委会在全校学生范围内,组织了一次传染病及个人卫生相关知识有奖竞赛(满分100分),竞赛奖励规则如下,得分在![]() 内的学生获三等奖,得分在
内的学生获三等奖,得分在![]() 内的学生获二等奖,得分在
内的学生获二等奖,得分在![]() 内的学生获一等奖,其他学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
内的学生获一等奖,其他学生不得奖.教务处为了解学生对相关知识的掌握情况,随机抽取了100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
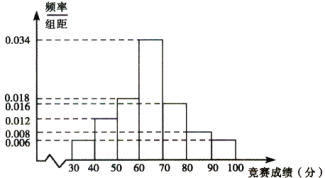
(1)现从该样本中随机抽取两名学生的竞赛成绩,求这两名学生中恰有一名学生获奖的概率;
(2)若该校所有参赛学生的成绩![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
为样本平均数的估计值,利用所得正态分布模型解决以下问题:
(i)若该校共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
(ii)若从所有参赛学生中(参赛学生数大于10000)随机抽取3名学生进行座谈,设其中竞赛成绩在64分以上的学生数为![]() ,求随机变量
,求随机变量![]() 的分布列和均值.
的分布列和均值.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村为了脱贫致富,引进了两种麻鸭品种,一种是旱养培育的品种,另一种是水养培育的品种.为了了解养殖两种麻鸭的经济效果情况,从中随机抽取500只麻鸭统计了它们一个季度的产蛋量(单位:个),制成了如图的频率分布直方图,且已知麻鸭的产蛋量在![]() 的频率为0.66.
的频率为0.66.
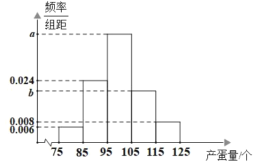
(1)求![]() ,
,![]() 的值;
的值;
(2)已知本次产蛋量近似服从![]() (其中
(其中![]() 近似为样本平均数,
近似为样本平均数,![]() 似为样本方差).若本村约有10000只麻鸭,试估计产蛋量在110~120的麻鸭数量(以各组区间的中点值代表该组的取值).
似为样本方差).若本村约有10000只麻鸭,试估计产蛋量在110~120的麻鸭数量(以各组区间的中点值代表该组的取值).
(3)若以正常产蛋90个为标准,大于90个认为是良种,小于90个认为是次种.根据统计得出两种培育方法的![]() 列联表如下,请完成表格中的统计数据,并判断是否有99.5%的把握认为产蛋量与培育方法有关.
列联表如下,请完成表格中的统计数据,并判断是否有99.5%的把握认为产蛋量与培育方法有关.
良种 | 次种 | 总计 | |
旱养培育 | 160 | 260 | |
水养培育 | 60 | ||
总计 | 340 | 500 |
附:![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
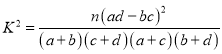 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com