
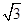 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.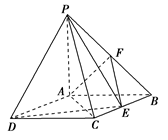
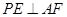 ;
;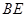 为何值时,
为何值时, 与平面
与平面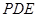 所成角的大小为45°.
所成角的大小为45°.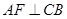 ,因为AF⊥PB所以AF⊥面PBC有
,因为AF⊥PB所以AF⊥面PBC有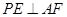 (3)
(3)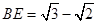
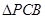 的中位线,
的中位线,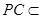 面PAC,
面PAC,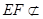 面PAC,所以EF//面PAC 4分
面PAC,所以EF//面PAC 4分 面PAB,所以
面PAB,所以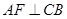 ,
,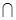 CB=B,所以AF⊥面PBC.
CB=B,所以AF⊥面PBC. 面PBC,所以无论点E在BC上何处,都有
面PBC,所以无论点E在BC上何处,都有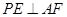 8分
8分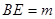 ,
, ,
,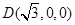 ,
,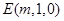 ,设面PDE的法向量为
,设面PDE的法向量为 ,
,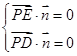 ,得
,得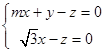 ,取
,取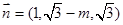 ,又
,又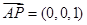 ,
,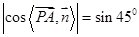 ,得
,得 ,解得
,解得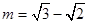 .
.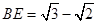 时,PA与面PDE成
时,PA与面PDE成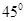 角 12分
角 12分

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源:不详 题型:解答题
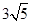 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
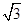 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将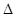 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为 ( ) 
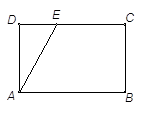
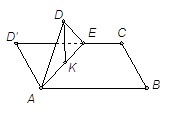
A.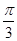 | B.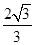 | C.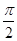 | D.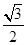 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
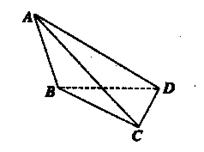
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.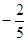 | B.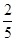 | C.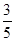 | D.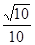 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com