
【题目】某家具公司生产甲、乙两种书柜,制柜需先制白胚再油漆,每种柜的制造白胚工时数、油漆工时数的有关数据如下:
工艺要求 | 产品甲 | 产品乙 | 生产能力(工时/天) |
制白胚工时数 | 6 | 12 | 120 |
油漆工时数 | 8 | 4 | 64 |
单位利润 | 20元 | 24元 |
则该公司合理安排这两种产品的生产,每天可获得的最大利润为______.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点
的左焦点![]() ,直线
,直线![]() 与y轴交于点P.且与椭圆交于A,B两点.A为椭圆的右顶点,B在x轴上的射影恰为
与y轴交于点P.且与椭圆交于A,B两点.A为椭圆的右顶点,B在x轴上的射影恰为![]() 。
。
(1)求椭圆E的方程;
(2)M为椭圆E在第一象限部分上一点,直线MP与椭圆交于另一点N,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校为了解即将毕业的男大学生的身体状况检测了960名男大学生的体重(单位:![]() ),所得数据都在区间
),所得数据都在区间![]() 中,其频率分布直方图如图所示.图中从左到右的前3个小组的频率之比为
中,其频率分布直方图如图所示.图中从左到右的前3个小组的频率之比为![]() .
.
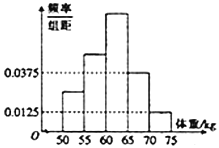
(1)求这960名男大学生中,体重小于![]() 的男大学生的人数;
的男大学生的人数;
(2)从体重在![]() 范围的男大学生中用分层抽样的方法选取6名,再从这6名男大学生中随机选取2名,记“至少有一名男大学生体重大于
范围的男大学生中用分层抽样的方法选取6名,再从这6名男大学生中随机选取2名,记“至少有一名男大学生体重大于![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】未来创造业对零件的精度要求越来越高.![]() 打印通常是采用数字技术材料打印机来实现的,常在模具制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有发展空间.某制造企业向
打印通常是采用数字技术材料打印机来实现的,常在模具制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有发展空间.某制造企业向![]() 高校
高校![]() 打印实验团队租用一台
打印实验团队租用一台![]() 打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取
打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取![]() 个零件,度量其内径的茎叶图如图(单位:
个零件,度量其内径的茎叶图如图(单位:![]() ).
).

(1)计算平均值![]() 与标准差
与标准差![]() ;
;
(2)假设这台![]() 打印设备打印出品的零件内径
打印设备打印出品的零件内径![]() 服从正态分布
服从正态分布![]() ,该团队到工厂安装调试后,试打了
,该团队到工厂安装调试后,试打了![]() 个零件,度量其内径分别为(单位:
个零件,度量其内径分别为(单位:![]() ):
):![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,试问此打印设备是否需要进一步调试?为什么?
,试问此打印设备是否需要进一步调试?为什么?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其它扣除.
其中,“基本减除费用”(免征额)为每年60000元.税率与速算扣除数见下表:
级数 | 全年应纳税所得额所在区间 | 税率( | 速算扣除数 |
1 |
| 3 | 0 |
2 |
| 10 | 2520 |
3 |
| 20 | 16920 |
… | … | … | … |
(1)设全年应纳税所得额为![]() 元,应缴纳个税税额为
元,应缴纳个税税额为![]() 元,求
元,求![]() ;
;
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老金、基本医疗保险费、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是![]() ,
,![]() ,
,![]() ,
,![]() ,专项附加扣除是52800元,依法确定其它扣除是4560元,那么他全年应缴纳多少综合所得个税?
,专项附加扣除是52800元,依法确定其它扣除是4560元,那么他全年应缴纳多少综合所得个税?
(3)设小王年综合所得收入额为![]() 元,应缴纳综合所得个税税额为
元,应缴纳综合所得个税税额为![]() 元,求
元,求![]() 关于
关于![]() 的函数解析式;并计算小王全年综合所得收入额由189600元增加到249600元,那么他全年缴纳多少综合所得个税?
的函数解析式;并计算小王全年综合所得收入额由189600元增加到249600元,那么他全年缴纳多少综合所得个税?
注:“综合所得”包括工资、薪金,劳务报酬,稿酬,特许权使用费;“专项扣除”包括居民个人按照国家规定的范围和标准缴纳的基本养老保险、基本医疗保险费、失业保险等社会保险费和住房公积金等;“专项附加扣除”包括子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等支出;“其他扣除”是指除上述基本减除费用、专项扣除、专项附加扣除之外,由国务院决定以扣除方式减少纳税的优惠政策规定的费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上,且不恒为零的函数
上,且不恒为零的函数![]() 满足:对于任意实数
满足:对于任意实数![]() 和
和![]() ,总有
,总有![]() 恒成立,则称
恒成立,则称![]() 为“类余弦型”函数.
为“类余弦型”函数.
(1)已知![]() 为“类余弦型”函数,且
为“类余弦型”函数,且![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)证明:函数![]() 为偶函数;
为偶函数;
(3)若![]() 为“类余弦型”函数,且对于任意非零实数
为“类余弦型”函数,且对于任意非零实数![]() ,总有
,总有![]() ,设有理数
,设有理数![]() 、
、![]() 满足
满足![]() ,判断
,判断![]() 和
和![]() 大小关系,并证明你的结论.
大小关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com