
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 周长为8.
周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() ,使以
,使以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,若存在求出直线
,若存在求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为等腰三角形.
为等腰三角形.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过左焦点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,其中
两点,其中![]()
![]() ,另一条过
,另一条过![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点(不与
两点(不与![]() 重合),且
重合),且![]() 点不与点
点不与点![]() 重合. 过
重合. 过![]() 作
作![]() 轴的垂线分别交直线
轴的垂线分别交直线![]() ,
,![]() 于
于![]() ,
,![]() .
.
①求![]() 点坐标; ②求证:
点坐标; ②求证:.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一片产量很大的水果种植园,在临近成熟时随机摘下某品种水果100个,其质量(均在l至11kg)频数分布表如下(单位: kg):
分组 | | | | | |
频数 | 10 | 15 | 45 | 20 | 10 |
以各组数据的中间值代表这组数据的平均值,将频率视为概率.
(1)由种植经验认为,种植园内的水果质量![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() 近似为样本方差
近似为样本方差![]() .请估算该种植园内水果质量在
.请估算该种植园内水果质量在![]() 内的百分比;
内的百分比;
(2)现在从质量为![]() 的三组水果中用分层抽样方法抽取14个水果,再从这14个水果中随机抽取3个.若水果质量
的三组水果中用分层抽样方法抽取14个水果,再从这14个水果中随机抽取3个.若水果质量![]() 的水果每销售一个所获得的的利润分别为2元,4元,6元,记随机抽取的3个水果总利润为
的水果每销售一个所获得的的利润分别为2元,4元,6元,记随机抽取的3个水果总利润为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:![]()
![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接2019年全国文明城市评比,某市文明办对市民进行了一次文明创建知识的网络问卷调查.每一位市民有且仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,文明办为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节期间爆发的新型冠状病毒(COVID-19)是新中国成立以来感染人数最多的一次疫情.一个不知道自己已感染但处于潜伏期的甲从疫区回到某市过春节,回到家乡后与朋友乙、丙、丁相聚过,最终乙、丙、丁也感染了新冠病毒.可以肯定的是乙受甲感染的,丙是受甲或乙感染的,假设他受甲和受乙感染的概率分别是![]() 和
和![]() .丁是受甲、乙或丙感染的,假设他受甲、乙和丙感染的概率分别是
.丁是受甲、乙或丙感染的,假设他受甲、乙和丙感染的概率分别是![]() 、
、![]() 和
和![]() .在这种假设之下,乙、丙、丁中直接受甲感染的人数为
.在这种假设之下,乙、丙、丁中直接受甲感染的人数为![]() .
.
(1)求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)该市在发现在本地出现新冠病毒感染者后,迅速采取应急措施,其中一项措施是各区必须每天及时,上报新增疑似病例人数.![]() 区上报的连续
区上报的连续![]() 天新增疑似病例数据是“总体均值为
天新增疑似病例数据是“总体均值为![]() ,中位数
,中位数![]() ”,
”,![]() 区上报的连续
区上报的连续![]() 天新增疑似病例数据是“总体均值为
天新增疑似病例数据是“总体均值为![]() ,总体方差为
,总体方差为![]() ”.设
”.设![]() 区和
区和![]() 区连续
区连续![]() 天上报新增疑似病例人数分别为
天上报新增疑似病例人数分别为![]() 和
和![]() ,
,![]() 和
和![]() 分别表示
分别表示![]() 区和
区和![]() 区第
区第![]() 天上报新增疑似病例人数(
天上报新增疑似病例人数(![]() 和
和![]() 均为非负).记
均为非负).记![]() ,
,![]() .
.
①试比较![]() 和
和![]() 的大小;
的大小;
②求![]() 和
和![]() 中较小的那个字母所对应的
中较小的那个字母所对应的![]() 个数有多少组?
个数有多少组?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某商场2018年洗衣机、电视机和电冰箱三种电器各季度销量的百分比堆积图(例如:第3季度内,洗衣机销量约占![]() ,电视机销量约占
,电视机销量约占![]() ,电冰箱销量约占
,电冰箱销量约占![]() ).根据该图,以下结论中一定正确的是( )
).根据该图,以下结论中一定正确的是( )
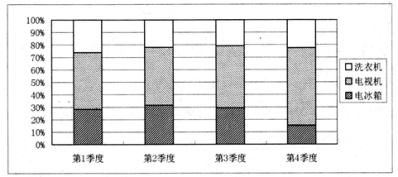
A. 电视机销量最大的是第4季度
B. 电冰箱销量最小的是第4季度
C. 电视机的全年销量最大
D. 电冰箱的全年销量最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,M,M1分别为AB,A1B1中点.

(1)求证:C1M1∥面A1MC;
(2)若面ABC⊥面ABB1A1,△AB1B为正三角形,AB=2,BC=1,![]() ,求四棱锥B1﹣AA1C1C的体积.
,求四棱锥B1﹣AA1C1C的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+acosx.
(1)求函数f(x)的奇偶性.并证明当|a|≤2时函数f(x)只有一个极值点;
(2)当a=π时,求f(x)的最小值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com