Question

【题目】已知全集U=R，集合A={x|0＜log2x＜2}，B={x|x≤3m﹣4或x≥8+m}（m＜6）．
（1）若m=2，求A∩（UB）；
（2）若A∩（UB）=，求实数m的取值范围．

Answer 1

【答案】
（1）解：全集U=R，集合A={x|0＜log2x＜2}={x|1＜x＜4}，

B={x|x≤3m﹣4或x≥8+m}（m＜6）；

当m=2时，B={x|x≤2或x≥10}，

∴UB={x|2＜x＜10}，

A∩（UB）={x|2＜x＜4}；

（2）解：UB={x|3m﹣4＜x＜8+m}，

当UB=时，3m﹣4≥8+m，解得m≥6，不合题意，舍去；

当UB≠时，应满足 ，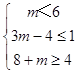

解得﹣4≤m≤ ，

∴实数m的取值范围是﹣4≤m≤ ．

【解析】（1）m=2时，求出集合B，根据补集与交集的定义计算即可；（2）求出UB，讨论UB=和UB≠时，对应实数m的取值范围．
【考点精析】认真审题，首先需要了解交、并、补集的混合运算(求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的思想方法)．