
| A. | $\frac{\sqrt{7}}{4}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 根据|F1F2|是|PF1|与|PF2|的等差中项,得到2|F1F2|=|PF1|+|PF2|,即|PF1|+|PF2|=4,得到点P在以F1,F2为焦点的椭圆上,已知a,c的值,即可求出动点P所形成的轨迹的离心率.
解答 解:∵F1(-1,0)、F2(1,0),
∴|F1F2|=2,
∵|F1F2|是|PF1|与|PF2|的等差中项,
∴2|F1F2|=|PF1|+|PF2|,
即|PF1|+|PF2|=4,
∴点P在以F1,F2为焦点的椭圆上,
∵2a=4,∴a=2
∵c=1
∴e=$\frac{c}{a}$=$\frac{1}{2}$.
故选:C.
点评 本题主要考查了应用椭圆的定义以及等差中项的概念求动点P所形成的轨迹的离心率,关键是求a,c的值.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 原点对称 | B. | x轴对称 | C. | y轴对称 | D. | 直线y=x对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
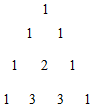 已知杨辉三角,将第4行的第一个数乘以1,第2个数乘以2,第3个数乘以4,第4个数乘以8后,这一行所以所有数字之和等于27(用数字作答):若等比数列{an}的前项是a1,公比是q(q≠1),将杨辉三角的第n+1行的第1个数乘以a1,第2个数乘以a2,…,第n+1个数乘以an+1后,这一行所有数字之和等于a1(1+q)n(用a1,q.n表示)
已知杨辉三角,将第4行的第一个数乘以1,第2个数乘以2,第3个数乘以4,第4个数乘以8后,这一行所以所有数字之和等于27(用数字作答):若等比数列{an}的前项是a1,公比是q(q≠1),将杨辉三角的第n+1行的第1个数乘以a1,第2个数乘以a2,…,第n+1个数乘以an+1后,这一行所有数字之和等于a1(1+q)n(用a1,q.n表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-∞,1) | C. | [2,+∞) | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com