
分析 求函数的导数,然后根据导数与函数单调区间的关系对a的大小进行分类讨论.
解答 解:函数的定义域为[0,+∞),
函数的f(x)的导数f′(x)=$\frac{1}{2\sqrt{x}}$-$\frac{1}{x+a}$,
令f′(x)=0,
即x2+(2a-4)x+a2=0,
其中△=4(a-2)2-4a2=8-8a,
(i)当a>1时,△<0成立,
对所有x>0,有x2+(2a-4)+a2>0.
即f′(x)>0,
此时f(x)在(0,+∞)内单调递增;
(ii)当a=1时,△=0成立,
对x≠1,有x2+(2a-4)x+a2>0,
即f′(x)>0,
此时f(x)在(0,1)内单调递增,且在(1,+∞)内也单调递增,
又知函数f(x)在x=1处连续,
因此,函数f(x)在(0,+∞)内单调递增;
(iii)当0<a<1时,△>0成立,
令f′(x)>0,
即x2+(2a-4)x+a2>0,
解得x<2-a-2$\sqrt{1-a}$或x>2-a+2$\sqrt{1-a}$,
因此,函数f(x)在区间$(0,2-a-2\sqrt{1-a})$,$(2-a+2\sqrt{1-a},+∞)$内也单调递增.
令f′(x)<0,
即x2+(2a-4)x+a2<0,
解得$2-a-2\sqrt{1-a}<x<2-a+2\sqrt{1-a}$,
因此,函数f(x)在区间$(2-a-2\sqrt{1-a},2-a+2\sqrt{1-a})$内单调递减.
点评 本题主要考查函数单调性的判断,根据函数单调性和导数之间的关系是解决本题的关键.考查学生应用导数研究函数单调性的方法及推理和运算能力.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(理)试卷(解析版) 题型:解答题
函数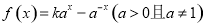 是定义在实数集
是定义在实数集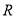 上的奇函数.
上的奇函数.
(1)若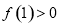 ,试求不等式
,试求不等式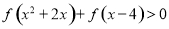 的解集;
的解集;
(2)若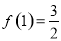 且
且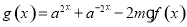 在
在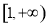 上的最小值为-2,求
上的最小值为-2,求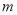 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1+2 | C. | 1+2+22 | D. | 1+2+22+23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com