练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．命题“存在x0∈R+，使log2x0≤0”的否定是（　　）
    A．不存在x0∈R+，使log2x0＞0B．对任意的x∈R+，有log2x＞0
    C．对任意的x∈R+，有log2x≤0D．存在x0∈R+，使log2x0＞0

    分析 利用特称命题的否定是全称命题写出结果即可．

    解答 解：特称命题“存在x0∈R+，使log2x0≤0”的否定是全称命题“对任意的x∈R+，有log2x＞0“，
    故选B．

    点评 本题考查命题的否定，注意量词的变化，基本知识的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知圆的半径为πcm，则120°的圆心角所对的弧长是（　　）
    A．$\frac{π}{3}$cmB．$\frac{{π}^{2}}{3}$cmC．$\frac{2π}{3}$cmD．$\frac{2{π}^{2}}{3}$cm

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知函数$f（x）=\left\{\begin{array}{l}lgx，x≥1\\ 1-3x，x＜1\end{array}\right.$，则f（f（-3））=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知函数f（x）=2x+x2-xln2-2，若函数g（x）=|f（x）|-loga（x+2）（a＞1）在区间[-1，1]上有4个不同的零点，则实数a的取值范围是（　　）
    A．（1，2）B．（2，+∞）C．[3${\;}^{\frac{1}{1-ln2}}$，+∞）D．（2，3${\;}^{\frac{1}{1-ln2}}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

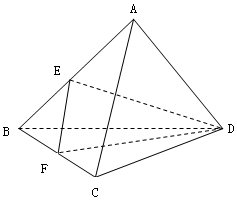    7．如图，已知正三棱锥A-BCD中，E、F分别是棱AB、BC的中点，EF⊥DE，且BC=2．
    （1）求此正三棱锥的体积；
    （2）求DE与平面ABC所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知圆C的方程是x2+y2-6x+5=0，则圆C的圆心和半径分别为（　　）
    A．（-3，0），2B．（3，0），2C．（-3，0），$\sqrt{2}$D．（3，0），$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．函数f（x）=$\left\{\begin{array}{l}{lnx（x＞0）}\\{-\sqrt{-x}（x≤0）}\end{array}\right.$与g（x）=$\frac{1}{2}$（|x+a|+1）的图象上存在关于y轴对称的点，则实数a的取值范围是（　　）
    A．（-∞，3-2ln2]B．[3-2ln2，+∞）C．[$\sqrt{e}$，+∞）D．（-∞，$-\sqrt{e}$]

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年江西省南昌市高二理下学期期末考试数学试卷（解析版） 题型：解答题

    面对某种流感病毒，各国医疗科研机构都在研究疫苗，现有A、B、C三个独立的研究机构在一定的时期研制出疫苗的概率分别为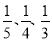．求:

    （1）他们能研制出疫苗的概率；

    （2）至多有一个机构研制出疫苗的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=x3+x，g（x）=ln（x+1）+$\frac{a{x}^{2}+ax-1}{x+1}$，其中a≥-$\frac{5}{16}$．
    （Ⅰ）对任意实数a，b，c，满足a+b，b+c，c+a都是非负数，判断f（a）+f（b）+f（c）的正负号，并证明你的结论；
    （Ⅱ）若对任意的x1∈[1，3]，存在x2∈[1，3]，使得f（x1）≥g（x2）成立，求a的取值范围；
    （Ⅲ）是否存在实数a，对任意的x1，x2∈[1，3]都有f（x1）≥g（x2）成立？若存在，求出a的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案