
【题目】已知数列![]() 满足:
满足: ![]() ,
, 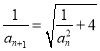 ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,试确定
,试确定![]() 的值,使得数列
的值,使得数列![]() 为等差数列;
为等差数列;
(3)将数列![]() 中的部分项按原来顺序构成新数列
中的部分项按原来顺序构成新数列![]() ,且
,且![]() ,求证:存在无数个满足条件的无穷等比数列
,求证:存在无数个满足条件的无穷等比数列![]() .
.
【答案】(1)![]() (
(![]() )(2)见解析(3)见解析
)(2)见解析(3)见解析
【解析】试题分析:(1)因为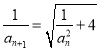 ,所以
,所以![]() , 数列
, 数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,从而求出通项公式;(2)因为
的等差数列,从而求出通项公式;(2)因为![]() ,即数列
,即数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,所以
的等差数列,所以![]() ,计算
,计算![]() ,利用
,利用![]() ,即可求出;(3)因为
,即可求出;(3)因为![]() ,
, ![]() ,先证数列
,先证数列![]() 满足题意,即证此数列中的任何一项都是数列
满足题意,即证此数列中的任何一项都是数列![]() 中的项. 令
中的项. 令![]() ,则只需证
,则只需证![]() 即可.本题也可考虑数学归纳法证明.
即可.本题也可考虑数学归纳法证明.
试题解析:
(1)因为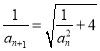 ,所以
,所以![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
所以, ![]() ,又由题意,
,又由题意, ![]() ,
,
所以![]() (
(![]() ).
).
(2)由![]() ,得
,得![]() ,
,
故![]() ,即数列
,即数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,
所以, ![]() ,令
,令![]() ,
, ![]() ,得
,得![]() ,
, ![]() .
.
若![]() 为等差数列,则
为等差数列,则![]() ,解得
,解得![]() .
.
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 为等差数列.
为等差数列.
所以,当![]() 时,数列
时,数列![]() 为等差数列.
为等差数列.
(3)![]() ,
, ![]() ,先证数列
,先证数列![]() 满足题意,即证此数列中的任何一项都是数列
满足题意,即证此数列中的任何一项都是数列![]() 中的项.
中的项.
令![]() ,则只需证
,则只需证![]() 即可.
即可.
此时, ![]() ,故
,故![]() .
.
所以,此数列![]() 中的第
中的第![]() 项是数列
项是数列![]() 中的第
中的第![]() 项.
项.
(也可以用数学归纳法证明![]() 能被
能被![]() 整除,证明如下)
整除,证明如下)
① 当![]() 时,
时, ![]() ,能被
,能被![]() 整除;
整除;
② 假设当![]() (
(![]() )时结论成立,即
)时结论成立,即![]() 能被
能被![]() 整除,
整除,
那么当![]() 时,
时, ![]() ,
,
因为![]() 与
与![]() 都能被
都能被![]() 整除,所以
整除,所以![]() 也能被
也能被![]() 整除,
整除,
即![]() 时,结论也成立.
时,结论也成立.
由①、②知,当![]() 时,
时, ![]() 能被
能被![]() 整除.
整除.
因此,以![]() 为首项,
为首项, ![]() ,
, ![]() ,…,
,…, ![]() ,…为公比的无穷等比数列均满足题意,命题得证.
,…为公比的无穷等比数列均满足题意,命题得证.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】数列![]() :
: ![]() 满足:
满足: ![]() ,
, ![]() 或1(
或1(![]() ).对任意
).对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() .,其中
.,其中![]()
![]() 且两两不相等.
且两两不相等.
(I)若![]() .写出下列三个数列中所有符合题目条件的数列的序号;
.写出下列三个数列中所有符合题目条件的数列的序号;
①1,1,1,2,2,2;②1,1,1,1,2,2,2,2;③1,l,1,1,1,2,2,2,2
(Ⅱ)记![]() .若
.若![]() ,证明:
,证明: ![]() ;
;
(Ⅲ)若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,圆
,圆![]() :
:![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(![]() ) 求直线
) 求直线![]() 的方程;
的方程;
(![]() )求直线
)求直线![]() 的斜率
的斜率![]() 的取值范围;
的取值范围;
(Ⅲ)是否存在过点![]() 且垂直平分弦
且垂直平分弦![]() 的直线
的直线![]() ?若存在,求直线
?若存在,求直线![]() 斜率
斜率![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
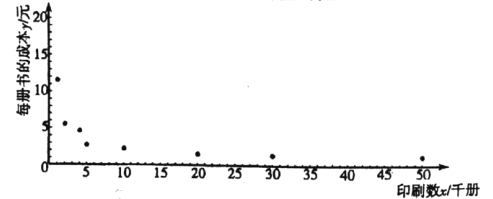
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.

表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少千册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为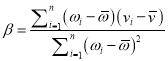 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com