
【题目】在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷,他必选1号,不选2号,另在3至5号中随机选2名.观众乙对5位歌手的演唱没有偏爱,因此在1至5号中随机选3名歌手.
(1)求观众甲选中3号歌手的概率;
(2)![]() 表示3号歌手得到观众甲、乙的票数之和,求
表示3号歌手得到观众甲、乙的票数之和,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由于观众甲必选1,不选2,则观众甲选中3号歌手的概率为![]() .
.
(2)![]() 表示观众甲、乙只有一人投票给3号歌手,分别求出观众甲投票给3号歌手,而乙没有投票给3号歌手和观众乙投票给3号歌手,而甲没有投票给3号歌手的投票方法总数,从而得出答案.
表示观众甲、乙只有一人投票给3号歌手,分别求出观众甲投票给3号歌手,而乙没有投票给3号歌手和观众乙投票给3号歌手,而甲没有投票给3号歌手的投票方法总数,从而得出答案.
(1)设A表示事件“观众甲选中3号歌手”
观众甲是1号歌手的歌迷,他必选1号,不选2号,则观众甲选3名歌手有![]() 种选法.
种选法.
观众甲选中3号歌手有![]() 种选法.
种选法.
所以观众甲选中3号歌手的概率![]()
(2)![]() 表示3号歌手得到观众甲、乙的票数之和,
表示3号歌手得到观众甲、乙的票数之和,
![]() 表示观众甲、乙只有一人投票给3号歌手.
表示观众甲、乙只有一人投票给3号歌手.
观众甲投票给3号歌手,而乙没有投票给3号歌手有![]() 种
种
观众乙投票给3号歌手,而甲没有投票给3号歌手有![]() 种
种
![]()


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
【题目】设四边形![]() 为矩形,点
为矩形,点![]() 为平面
为平面![]() 外一点,且
外一点,且![]() 平面
平面![]() ,若
,若![]() ,
,![]() .
.
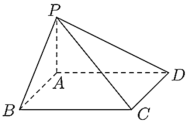
(1)求![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(2)在![]() 边上是否存在一点
边上是否存在一点![]() ,使得点
,使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若点![]() 是
是![]() 的中点,在
的中点,在![]() 内确定一点
内确定一点![]() ,使
,使![]() 的值最小,并求此时
的值最小,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年数学竞赛请自以为来自X星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题;然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答的题目则跳过(例如,他可以按照9,8,7,4,3,2,1,5,6,10的次序答题),这样所有的题目均有作答,设这位选手可能的答题次序有n种,则n的值为( )
A.512B.511C.1024D.1023
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设锐角![]() 的外接圆的半径为
的外接圆的半径为![]() ,在
,在![]() 内取外接圆的同心圆
内取外接圆的同心圆![]() ,其半径为
,其半径为![]()
![]() ,从圆
,从圆![]() 上任取一点
上任取一点![]() ,作
,作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
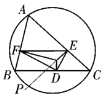
(1)求证:![]() 的面积为定值;
的面积为定值;
(2)猜想:当![]() 为任意三角形、同心圆
为任意三角形、同心圆![]() 为任意同心圆时,结论是否成立(不要求证明)?
为任意同心圆时,结论是否成立(不要求证明)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题,测试前根据对学生的了解,预估了每道题的难度,如表所示:
为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题,测试前根据对学生的了解,预估了每道题的难度,如表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了20名学生的答题数据进行统计,结果如表:

(Ⅰ)根据题中数据,估计中240名学生中第5题的实测答对人数;
(Ⅱ)从抽样的20名学生中随机抽取2名学生,记这2名学生中第5题答对的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)试题的预估难度和实测难度之间会有偏差.设![]() 为第
为第![]() 题的实测难度,请用
题的实测难度,请用![]() 和
和![]() 设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.
设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中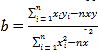 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com