
 中,三角形
中,三角形 是边长为4的正三角形,
是边长为4的正三角形, ,
, 平面
平面 ,
, .
. 是
是 的中点,求证:
的中点,求证:
 ;
; 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.
 的中点为
的中点为 ,由
,由 平面
平面 得:
得: ,
, ,所以
,所以 是正方形,点
是正方形,点 是线段
是线段 的中点,
的中点, ,所以
,所以 ,……………………………………………………2分
,……………………………………………………2分 平面
平面 得:
得: ,…………………………………………………3分
,…………………………………………………3分 ,所以
,所以 ,且
,且 ,
,
 ,所以
,所以 ,………………………………………………5分
,………………………………………………5分 平面
平面 ,所以
,所以
 ;……………………………………6分
;……………………………………6分 为原点,
为原点, 所在方向分别为
所在方向分别为 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系 ,则
,则 , --------8分
, --------8分
 的法向量为
的法向量为 ,则有
,则有
 ,
,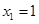 ,则
,则 …………………………10分
…………………………10分 的法向量为
的法向量为 ,则有
,则有
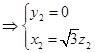 ,令
,令 ,则
,则 …………………………………12分
…………………………………12分 ,
, 与平面
与平面 所成的角的余弦值是
所成的角的余弦值是 。…………………………14分
。…………………………14分

科目:高中数学 来源:不详 题型:解答题
 .
.
 ,EF =
,EF =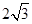 ,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?
,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
, 是两个不同的平面,m ,n 是两条不同的直线,则下列正确的是
是两个不同的平面,m ,n 是两条不同的直线,则下列正确的是A.若m // ,? ,?   =" n" ,则m //n =" n" ,则m //n |
B.若m⊥ ?,n ?,n  ,m ⊥n ,则 ,m ⊥n ,则 ⊥ ⊥ ? ? ? ? |
C.若 // // ,m⊥ ,m⊥ ,n // ,n // ,则m⊥n ,则m⊥n |
D.若 ⊥ ⊥ , ,   =" m" ,m //n,则n // =" m" ,m //n,则n // |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 与平面
与平面 相交与一点A,则下列结论正确的是( )
相交与一点A,则下列结论正确的是( )A. 内的所有直线与 内的所有直线与 异面 异面 | B. 内不存在与 内不存在与 平行的直线 平行的直线 |
C. 内存在唯一的直线与 内存在唯一的直线与 平行 平行 | D. 内的直线与 内的直线与 都相交 都相交 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,
的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,  ,
, .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

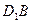 与平面
与平面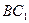 所成角的正切值
所成角的正切值查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com