解:(1)∵f(y-x+1)=f(x)f(y)+f(x-1)f(y-1).
∴令y=x-1,得f(0)=f(x)f(x-1)+f(x-1)f(x-2).
再令x=1,代入上式得:f(0)=f(1)f(0)+f(0)f(-1).
∴f(0)[1-f(1)-f(-1)]=0.
∵f(1)=1>0>f(-1)
∴1-f(1)-f(-1)≠0
∴f(0)=0,
由上面的证明,得f(x)f(x-1)+f(x-1)f(x-2)=0.
即f(x-1)[f(x)+f(x-2)]=0,而f(x-1)不恒等于0
故f(x)+f(x-2)=0恒成立
对上式令x=3,得f(3)+f(1)=0?f(3)=-f(1)=-1
(2)对f(y-x+1)=f(x)f(y)+f(x-1)f(y-1)令y=0,得
f(-x+1)=f(x)f(0)+f(x-1)f(-1)
由(1)得,f(-1)=-f(-1+2)=-1,f(0)=0
∴f(-x+1)=-f(x-1),即f(-x)=-f(x),
∴函数为奇函数
(3)f(1-2x)=f(-x-x+1)=-f
2(x)+f(x-1)f(-x-1)
∴
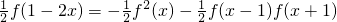
∴
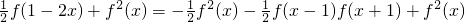
=
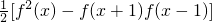
∵f
2(x)=1-f
2(x-1)?f
2(x)-f(x+1)f(x-1)=1-f(x-1)[f(x-1)+f(x+1)]
而f(x-1)+f(x+1)=0,所以f
2(x)-f(x+1)f(x-1)=1
∴
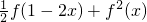
=

分析:(1)将已知等式中令y=1,变形再令x=1,可得f(0)[1-f(1)-f(-1)]=0.再根据f(1)=1>0>f(-1),得
1-f(1)-f(-1)≠0,得f(0)=0,再根据f(x-1)[f(x)+f(x-2)]=0,而f(x-1)不恒等于0,故f(x)+
f(x-2)=0恒成立对上式令x=3,得f(3)+f(1)=0?f(3)=-f(1)=-1.
(2)对f(y-x+1)=f(x)f(y)+f(x-1)f(y-1)令y=0,得f(-x+1)=f(x)f(0)+f(x-1)f(-1),
再根据(1)得,f(-1)=-f(-1+2)=-1,f(0)=0,从而f(-x+1)=-f(x-1),即f(-x)=-f(x),函数为奇函数.
(3)令y=-x代入条件中的等式,可得f(1-2x)=f(-x-x+1)=-f
2(x)+f(x-1)f(-x-1),再利用函数为奇函数的性质,结合条件得f
2(x)-f(x+1)f(x-1)=1,代入即得
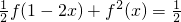
.
点评:本题考查了函数奇偶性的判断,和抽象函数的性质和求值的问题,属于难题.合理地利用条件赋值,是解决本题的关键所在.

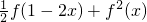 的值.
的值.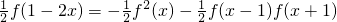
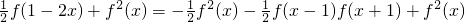
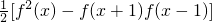
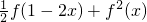 =
=
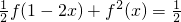 .
.

 附加题:
附加题: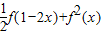 的值.
的值.