
【题目】已知函数f(x)=x2+bx+c,其对称轴为y轴(其中b,c为常数) (Ⅰ)求实数b的值;
(Ⅱ)记函数g(x)=f(x)﹣2,若函数g(x)有两个不同的零点,求实数c的取值范围;
(Ⅲ)求证:不等式f(c2+1)>f(c)对任意c∈R成立.
【答案】解:(Ⅰ)∵函数f(x)=x2+bx+c,其对称轴为y轴, ∴ ![]() =0,
=0,
解得:b=0;
(Ⅱ)由(I)得:f(x)=x2+c,
则g(x)=f(x)﹣2=x2+c﹣2,
若函数g(x)有两个不同的零点,
则△=﹣4(c﹣2)>0,
解得:c<2;
(Ⅲ)证明:函数f(x)=x2+c的开口朝上,
∵|c2+1|2﹣|c|2=c4+c2+1=(c2+ ![]() )2+
)2+ ![]() >0恒成立,
>0恒成立,
故|c2+1|>|c|,
故不等式f(c2+1)>f(c)对任意c∈R成立
【解析】(Ⅰ)若函数f(x)=x2+bx+c,其对称轴为y轴,则 ![]() =0,解得b值; (Ⅱ)由(I)得g(x)=f(x)﹣2=x2+c﹣2,若函数g(x)有两个不同的零点,则△=﹣4(c﹣2)>0,解得c的范围; (Ⅲ)函数f(x)=x2+c的开口朝上,证得|c2+1|2﹣|c|2>0恒成立,可得不等式f(c2+1)>f(c)对任意c∈R成立.
=0,解得b值; (Ⅱ)由(I)得g(x)=f(x)﹣2=x2+c﹣2,若函数g(x)有两个不同的零点,则△=﹣4(c﹣2)>0,解得c的范围; (Ⅲ)函数f(x)=x2+c的开口朝上,证得|c2+1|2﹣|c|2>0恒成立,可得不等式f(c2+1)>f(c)对任意c∈R成立.


科目:高中数学 来源: 题型:
【题目】某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是岁. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本,(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出如下频率分布直方图.
的分组作出如下频率分布直方图.
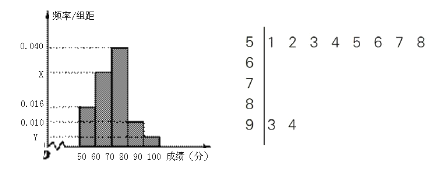
(1)由如下茎叶图(图中仅列出了得分在![]() ,
,![]() 的数据)提供的信息,求样本容量
的数据)提供的信息,求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国谜语大会”,求所抽取的2名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)=3sin(2x+φ)的图象关于点( ![]() ,0)成中心对称(|φ|<
,0)成中心对称(|φ|< ![]() ),那么函数f(x)图象的一条对称轴是( )
),那么函数f(x)图象的一条对称轴是( )
A.x=﹣ ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个体户计划经销A、B两种商品,据调查统计,当投资额为x(x≥0)万元时,在经销A、B商品中所获得的收益分别为f(x)万元与g(x)万元、其中f(x)=a(x﹣1)+2(a>0);g(x)=6ln(x+b),(b>0)已知投资额为零时,收益为零.
(1)试求出a、b的值;
(2)如果该个体户准备投入5万元经营这两种商品,请你帮他制定一个资金投入方案,使他能获得最大收益,并求出其收入的最大值.(精确到0.1,参考数据:ln3≈1.10).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的程序框图表示的算法中,输入三个实数a,b,c,要求输出的x是这三个数中最大的数,那么在空白的判断框中,应该填入( ) 
A.x>c
B.c>x
C.c>b
D.c>a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设α是空间中的一个平面,l,m,n是三条不同的直线,则下列命题中正确的是( )
A.若mα,nα,l⊥m,l⊥n,则l⊥α
B.若mα,n⊥α,l⊥n,则l∥m
C.若l∥m,m⊥α,n⊥α,则l∥n
D.若l⊥m,l⊥n,则n∥m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,过点
中,过点![]() 的直线
的直线![]() 的倾斜角为45°,以坐标原点为极点,
的倾斜角为45°,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 和曲线
和曲线![]() 的交点为点
的交点为点![]() .
.
(1)求直线![]() 的参数方程;
的参数方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com