
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .
.
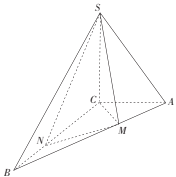
(1)证明:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)证明BC⊥平面SAC,即可推出SC⊥平面ABC,从而得到MN⊥平面SCM,即可证明MN⊥SM.(2)以C为原点,以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,求出平面SAM和平面SMN的法向量,利用空间向量的夹角的余弦,求解二面角A﹣SM﹣N的余弦值.
,求出平面SAM和平面SMN的法向量,利用空间向量的夹角的余弦,求解二面角A﹣SM﹣N的余弦值.
(1)证明:由![]() ,
,![]() ,且
,且![]() ,则
,则![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() ,又
,又![]() ,
,![]() ,则
,则![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,故
,故![]() .
.
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,则
,则![]() .
.
(2)解:由(1)知,![]() ,
,![]() ,
,![]() 两两相互垂直,
两两相互垂直,
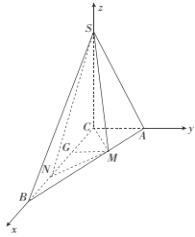
如图是以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
![]() ,令
,令![]() ,得
,得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,故
,故![]() .
.
所以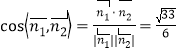 ,
,
由图可知二面角![]() 为钝角,
为钝角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】[2019·武汉六中]袋子中有四个小球,分别写有“武、汉、军、运”四个字,从中任取一个小球,有放回抽取,直到取到“军”“运”二字就停止,用随机模拟的方法估计恰好在第三次停止的概率:利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“军、运、武、汉”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下16组随机数:
232 321 230 023 123 021 132 220
231 130 133 231 331 320 122 233
由此可以估计,恰好第三次就停止的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在二项式![]() 的展开式中,
的展开式中,
(1)若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项的系数;(最后结果用算式表达,不用计算出数值)
(2)若展开式前三项的二项式系数的和等于79,求展开式中系数最大的项.(最后结果用算式表达,不用计算出数值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机作为客户端越来越为人们所青睐,通过手机实现衣食住行消费已经成为一种主要的消费方式.在某市,随机调查了200名顾客购物时使用手机支付的情况,得到如下的2×2列联表,已知从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
(I)根据已知条件完成2×2列联表,并根据此资料判断是否有99.5%的把握认为“市场购物用手机支付与年龄有关”?
2×2列联表:
青年 | 中老年 | 合计 | |
使用手机支付 | 120 | ||
不使用手机支付 | 48 | ||
合计 | 200 |
(Ⅱ)现采用分层抽样的方法从这200名顾客中按照“使用手机支付”和“不使用手机支付”抽取一个容量为10的样本,再从中随机抽取3人,求这三人中“使用手机支付”的人数的分布列及期望.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛.若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() 各局比赛结果相互独立.则甲在4局以内(含4局)赢得比赛的概率为( )
各局比赛结果相互独立.则甲在4局以内(含4局)赢得比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (t为参数),直线
(t为参数),直线![]() 的参数方程为
的参数方程为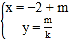 (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)写出![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设
轴正半轴为极轴建立极坐标系,设![]() ,
,![]() 为
为![]() 与
与![]() 的交点,求
的交点,求![]() 的极径.
的极径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com