
【题目】2019年高考刚过,为了解考生对全国2卷数学试卷难度的评价,随机抽取了某学校50名男考生与50名女考生,得到下面的列联表:
非常困难 | 一般 | |
男考生 | 20 | 30 |
女考生 | 40 | 10 |
(1)分别估计该学校男考生、女考生觉得全国2卷数学试卷非常困难的概率;
(2)从该学校随机抽取3名男考生,2名女考生,求恰有4名考生觉得全国2卷数学试卷非常困难的概率.
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)若![]() ,
,![]() ,求实数
,求实数![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,给出一个新数列
时,给出一个新数列![]() ,其中
,其中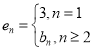 ,设这个新数列的前
,设这个新数列的前![]() 项和为
项和为![]() ,若
,若![]() 可以写成
可以写成![]() (
(![]() ,
,![]() 且
且![]() ,
,![]() )的形式,则称
)的形式,则称![]() 为“指数型和”.问
为“指数型和”.问![]() 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数)曲线
为参数)曲线![]() 的普通方程为
的普通方程为![]() ,以坐标原点为极点,以
,以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() 依次与曲线
依次与曲线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,射线
两点,射线![]() :
:![]() 依次与曲线
依次与曲线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
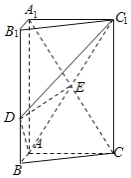
【题目】如图,三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() .
.
(1)试用空间向量证明直线![]() 与平面
与平面![]() 不平行;
不平行;
(2)设平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)在(2)的条件下,设平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 的所成角.
的所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着教育信息化2.0时代的到来,依托网络进行线上培训越来越便捷,逐步成为实现全民终身学习的重要支撑.最近某高校继续教育学院采用线上和线下相结合的方式开展了一次300名学员参加的“国学经典诵读”专题培训.为了解参训学员对于线上培训、线下培训的满意程度,学院随机选取了50名学员,将他们分成两组,每组25人,分别对线上、线下两种培训进行满意度测评,根据学员的评分(满分100分)绘制了如下茎叶图:
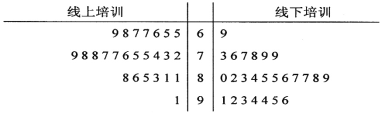
(1)根据茎叶图判断学员对于线上、线下哪种培训的满意度更高?并说明理由;
(2)求50名学员满意度评分的中位数![]() ,并将评分不超过
,并将评分不超过![]() 、超过
、超过![]() 分别视为“基本满意”、“非常满意”两个等级.
分别视为“基本满意”、“非常满意”两个等级.
(i)利用样本估计总体的思想,估算本次培训共有多少学员对线上培训非常满意?
(ii)根据茎叶图填写下面的列联表:
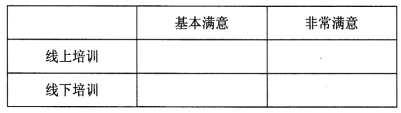
并根据列联表判断能否有99.5%的把握认为学员对两种培训方式的满意度有差异?
附: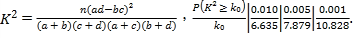
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,点
,点![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() 点.
点.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作斜率不为0的直线
作斜率不为0的直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com