
【题目】设函数f(x)的定义域为(-3,3),
满足f(-x)=-f(x),且对任意x,y,都有f(x)-f(y)=f(x-y),当x<0时,f(x)>0,f(1)=-2.
(1)求f(2)的值;
(2)判断f(x)的单调性,并证明;
(3)若函数g(x)=f(x-1)+f(3-2x),求不等式g(x)≤0的解集.
【答案】(1)f(2)=-4;(2)见解析;(3)(0,2].
【解析】试题分析:(1)通过赋值法,令x=2,y=1代入即得;
(2)利用单调性定义证明即可;
(3)由奇函数条件得到f(x-1)≤f(2x-3),结合单调性和定义即可解得.
试题解析:
(1)在f(x)-f(y)=f(x-y)中,
令x=2,y=1,代入得:f(2)-f(1)=f(1),所以f(2)=2f(1)=-4.
(2)f(x)在(-3,3)上单调递减.证明如下:
设-3<x1<x2<3,则x1-x2<0,
所以f(x1)-f(x2)=f(x1-x2)>0,
即f(x1)>f(x2),
所以f(x)在(-3,3)上单调递减.
(3)由g(x)≤0得f(x-1)+f(3-2x)≤0,
所以f(x-1)≤-f(3-2x).
又f(x)满足f(-x)=-f(x),
所以f(x-1)≤f(2x-3),
又f(x)在(-3,3)上单调递减,
所以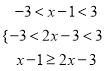 解得0<x≤2,
解得0<x≤2,
故不等式g(x)≤0的解集是(0,2].


科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 越大,说明“
越大,说明“![]() 与
与![]() 有关系”的可信度越大.
有关系”的可信度越大.
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为![]() 中,
中, ![]() ,
,
则![]() .正确的个数是( )
.正确的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2-a≤x≤2+a},B={x|x≤1或x≥4}.
(1)当a=3时,求A∩B;
(2)若a>0,且A∩B=![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区预计从2015年初开始的第![]() 月,商品
月,商品![]() 的价格
的价格![]() (
(![]() ,
, ![]() ,价格单位:元),且第
,价格单位:元),且第![]() 月该商品的销售量
月该商品的销售量![]() (单位:万件).
(单位:万件).
(1)商品![]() 在2015年的最低价格是多少?
在2015年的最低价格是多少?
(2)2015年的哪一个月的销售收入最少,最少是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为正常数.
为正常数.
⑴若![]() ,且
,且![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
⑵在⑴中当![]() 时,函数
时,函数![]() 的图象上任意不同的两点
的图象上任意不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,试证明:
,试证明: ![]() .
.
⑶若![]() ,且对任意的
,且对任意的![]() ,
, ![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三年级有3名男生和1名女生为了报某所大学,事先进行了多方详细咨询,并根据自己的高考成绩情况,最终估计这3名男生报此所大学的概率都是![]() ,这1名女生报此所大学的概率是
,这1名女生报此所大学的概率是![]() .且这4人报此所大学互不影响。
.且这4人报此所大学互不影响。
(Ⅰ)求上述4名学生中报这所大学的人数中男生和女生人数相等的概率;
(Ⅱ)在报考某所大学的上述4名学生中,记![]() 为报这所大学的男生和女生人数的和,试求
为报这所大学的男生和女生人数的和,试求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
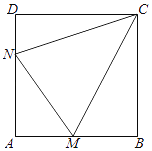
【题目】如图所示,某村积极开展“美丽乡村生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上. (Ⅰ)当点M,N分别是边AB,AD的中点时,求∠MCN的余弦值;
(Ⅱ)由于村建规划及保护生态环境的需要,要求△AMN的周长为2千米,请探究∠MCN是否为定值,若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com