
����Ŀ��ijУΪ�����һ���߶�ѧ�������ڼ�ѧϰ��ʱ����������ȡ�˸�һ���߶���![]() �ˣ������ǵ�ѧϰʱ�������ͳ�ƣ��ֱ�õ��˸�һѧ��ѧϰʱ�䣨��λ��Сʱ����Ƶ���ֲ����߶�ѧ��ѧϰʱ���Ƶ�ʷֲ�ֱ��ͼ.
�ˣ������ǵ�ѧϰʱ�������ͳ�ƣ��ֱ�õ��˸�һѧ��ѧϰʱ�䣨��λ��Сʱ����Ƶ���ֲ����߶�ѧ��ѧϰʱ���Ƶ�ʷֲ�ֱ��ͼ.
��һѧ��ѧϰʱ���Ƶ���ֲ�����ѧϰʱ���������![]() �ڣ���
�ڣ���
ѧϰʱ�� |
|
|
|
|
|
|
Ƶ�� | 3 | 1 | 8 | 4 | 2 | 2 |
�߶�ѧ��ѧϰʱ���Ƶ�ʷֲ�ֱ��ͼ��
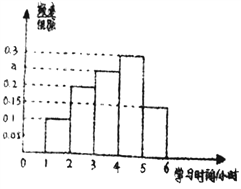
��1����߶�ѧ��ѧϰʱ���Ƶ�ʷֲ�ֱ��ͼ�е�![]() ֵ�������ݴ�Ƶ�ʷֲ�ֱ��ͼ���Ƹ�У�߶�ѧ��ѧϰʱ�����λ����
ֵ�������ݴ�Ƶ�ʷֲ�ֱ��ͼ���Ƹ�У�߶�ѧ��ѧϰʱ�����λ����
��2�����÷ֲ�����ķ������Ӹ�һѧ��ѧϰʱ����![]() ��
��![]() �������������ȡ
�������������ȡ![]() �����ٴ���
�����ٴ���![]() ���������ȡ
���������ȡ![]() ������ѧϰʱ����
������ѧϰʱ����![]() ��һ����������
��һ����������![]() �˱����еĸ���.
�˱����еĸ���.
���𰸡���1��![]() ��3.8����2��
��3.8����2��![]()
����������������1���������ʷֲ�ֱ��ͼ��������ֱ��ͼ�����֮��Ϊ1�ɵ�aֵ����2�����ݷֲ��������ɵã��Ӹ�һѧ��ѧϰʱ����![]() �г�ȡ
�г�ȡ![]() �ˣ��Ӹ�һѧ��ѧϰʱ����
�ˣ��Ӹ�һѧ��ѧϰʱ����![]() �г�ȡ
�г�ȡ![]() �ˣ�
�ˣ�
Ȼ����ݹŵ���ͼ��㹫ʽ�ɵý���.
��⣺
��1����ͼ��֪��ѧ��ѧϰʱ��������![]() �ڵ�Ƶ��Ϊ
�ڵ�Ƶ��Ϊ![]() ��
��
![]() �ڵ�Ƶ��Ϊ
�ڵ�Ƶ��Ϊ![]() ������
������![]()
����λ��Ϊ![]() ����
����![]() �����
�����![]() ��
��
����У�߶�ѧ��ѧϰʱ�����λ��Ϊ![]() .
.
��2�����ݷֲ�������Ӹ�һѧ��ѧϰʱ����![]() �г�ȡ
�г�ȡ![]() �ˣ��Ӹ�һѧ��ѧϰʱ����
�ˣ��Ӹ�һѧ��ѧϰʱ����![]() �г�ȡ
�г�ȡ![]() �ˣ�����
�ˣ�����![]() ���������ȡ
���������ȡ![]() �˹���
�˹���![]() �����������ѧϰʱ����
�����������ѧϰʱ����![]() ��һ����û�˱����е���
��һ����û�˱����е���![]() �����������
�����������![]() ��һ����������
��һ����������![]() �˱����е��¼�Ϊ
�˱����е��¼�Ϊ![]() ��
��
��![]() .
.


 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д� ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ ![]() �������ⳤ��Ϊ2��
�������ⳤ��Ϊ2�� ![]() Ϊ
Ϊ ![]() �е�.
�е�.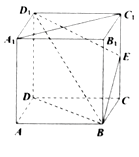
������֤�� ![]() ƽ��
ƽ�� ![]() ��
��
������ ![]() ����ƽ��
����ƽ�� ![]() ��ƽ��
��ƽ�� ![]() ���������ǵĴ�С.
���������ǵĴ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015��һ����ͳ����ij·�ι��������ij��ٴ�С�뷢���Ľ�ͨ�¹ʴ������õ����±���ʾ�����ݣ�

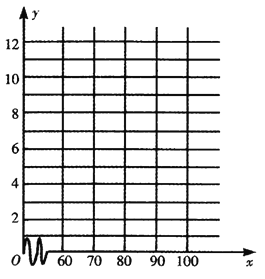
��1���뻭���ϱ����ݵ�ɢ��ͼ��
��2��������ϱ��ṩ�����ݣ�����С���˷����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��3���Ը��ݣ�2����������Իع鷽�̣�Ԥ����2016���·��·������ذ�ȫ��ʩ�Ȳ��������£����ٴﵽ110![]() ʱ�����ܷ����Ľ�ͨ�¹ʴ���.
ʱ�����ܷ����Ľ�ͨ�¹ʴ���.
������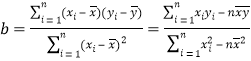 ��
��![]() ������
������![]() Ϊ����ƽ��ֵ��
Ϊ����ƽ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() sin��x��
sin��x�� ![]() cos��x���أ�0������y=f��x+
cos��x���أ�0������y=f��x+ ![]() ����ͼ����y=f��x��
����ͼ����y=f��x�� ![]() ����ͼ���غϣ��Ǧص����ֵΪ��0 �� ����g��x��=cos����0x��
����ͼ���غϣ��Ǧص����ֵΪ��0 �� ����g��x��=cos����0x�� ![]() ���ĵ�����������Ϊ�� ��
���ĵ�����������Ϊ�� ��
A.[�� ![]() ��+
��+ ![]() ����
���� ![]() +
+ ![]() ]��k��Z��
]��k��Z��
B.[�� ![]() +
+ ![]() ��
�� ![]() +
+ ![]() ]��k��Z��
]��k��Z��
C.[�� ![]() ��+2k����
��+2k���� ![]() +2k��]��k��Z��
+2k��]��k��Z��
D.[�� ![]() +2k����
+2k���� ![]() +2k��]��k��Z��
+2k��]��k��Z��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �У���������
����������![]() ����
����![]() ��
��![]() ���������������
Ϊ���������������![]() Ϊ���Ȳ�����С�������ԡ��Ȳ�����С� ���жϣ���
Ϊ���Ȳ�����С�������ԡ��Ȳ�����С� ���жϣ���![]() ������Ϊ
������Ϊ![]() ���ڵȲ�����һ���ǵȲ�����У� �۵ȱ�����һ���ǵȲ������ ����ͨ�ʽΪ
���ڵȲ�����һ���ǵȲ�����У� �۵ȱ�����һ���ǵȲ������ ����ͨ�ʽΪ![]() ������
������![]() ����
����![]() ��
��![]() ��������һ���ǵȲ�����У�������ȷ���ж��ǣ� ��
��������һ���ǵȲ�����У�������ȷ���ж��ǣ� ��
A. �٢ۢ� B. �ڢۢ� C. �٢� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����Ϊ����������{an}��ǰn���ΪSn �� ��Sn����n��n+1��Sn2+��n2+n��1��Sn��1=0��n��N*������S1+S2+��+S2017= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P(x,y)(����y ![]() )��x��ľ����������F(0,1)�ľ�����1.
)��x��ľ����������F(0,1)�ľ�����1.
��1����P�Ĺ켣���̣�
��2����ֱ��l��x-y+1=0�붯��P�Ĺ켣����A��B���㣬���OAB�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�� ![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬 ![]() ����Բ
����Բ ![]() �ϵ��������㣬����ֱ��
�ϵ��������㣬����ֱ�� ![]() ��ֱ��
��ֱ�� ![]() ����ֱ��
����ֱ�� ![]() �Գ�.
�Գ�.
��1��֤��ֱ�� ![]() ��б��Ϊ��ֵ������������ֵ��
��б��Ϊ��ֵ������������ֵ��
��2���� ![]() ��������ʱֱ��
��������ʱֱ�� ![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ ![]() ��Բ����ֱ��
��Բ����ֱ�� ![]() �ϣ���Բ
�ϣ���Բ ![]() ������
������ ![]() .
.
��1����Բ�ı����̣�
��2��ֱ�� ![]() ����
���� ![]() ����Բ
����Բ ![]() �ཻ�������ҳ�Ϊ4����ֱ��
�ཻ�������ҳ�Ϊ4����ֱ�� ![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com