
分析 (1)由a2+b2-2a-4b+5=0配方,求出a,b,由C=$\frac{π}{3}$,利用余弦定理求c的值;
(2)若sinA+sinB=$\frac{\sqrt{3}}{2}$,sinA=$\frac{\sqrt{3}}{6}$,sinB=$\frac{\sqrt{3}}{3}$,分类讨论求sinC的值.
解答 解:(1)∵a2+b2-2a-4b+5=0,
∴(a-1)2+(b-2)2=0,
∴a=1,b=2,
∵C=$\frac{π}{3}$,
∴c=$\sqrt{1+4-2×1×2×\frac{1}{2}}$=$\sqrt{3}$;
(2)∵a=1,b=2,
∴2sinA=sinB,
∵sinA+sinB=$\frac{\sqrt{3}}{2}$,
∴sinA=$\frac{\sqrt{3}}{6}$,sinB=$\frac{\sqrt{3}}{3}$,
∵a<b,
∴A<B,
∴cosA=$\frac{\sqrt{33}}{6}$,
B为锐角,则cosB=$\frac{\sqrt{6}}{3}$,sinC=sin(A+B)=$\frac{\sqrt{11}+\sqrt{2}}{6}$;
B为钝角,则cosB=-$\frac{\sqrt{6}}{3}$,sinC=sin(A+B)=$\frac{\sqrt{11}-\sqrt{2}}{6}$.
点评 本题考查余弦定理、正弦定理的运用,考查分类讨论的数学思想,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
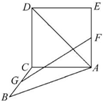 如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A. | 13种 | B. | 21种 | C. | 34种 | D. | 55种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
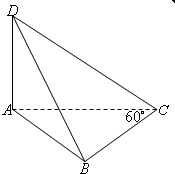 如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )
如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.28 | B. | 0.44 | C. | 0.56 | D. | 0.84 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com