

 =-2
=-2 ,求证:
,求证: +
+ +
+ =0;
=0; ·(
·( +
+ )的最小值.
)的最小值. =
= (
( +
+ ).代入
).代入 =-2
=-2 ,得
,得 =-
=- -
- ,即
,即 +
+ +
+ =0
=0  ·(
·( +
+ ),转化为-2|
),转化为-2| ||
|| |=2(x-1)2-2的形式,然后根据二次函数在定区间上的最值的求法,得到答案.
|=2(x-1)2-2的形式,然后根据二次函数在定区间上的最值的求法,得到答案. =
= (
( +
+ ) ..3分
) ..3分 =-2
=-2 ,得
,得 =-
=- -
- , .2分
, .2分 +
+ +
+ =0 1分
=0 1分 |=x,则|
|=x,则| |=2-x(0≤x≤2) .1分
|=2-x(0≤x≤2) .1分 +
+ =2
=2 2分
2分 ·(
·( +
+ )=2
)=2 ·
· =-2|
=-2| ||
|| |
|

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:填空题
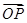 ·
·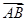 的最小值为________.
的最小值为________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com