
 如图,圆O和圆O'相交于A,B两点,AC是圆O'的切线,AD是圆O的切线,若BC=2,AB=4,则BD= .
如图,圆O和圆O'相交于A,B两点,AC是圆O'的切线,AD是圆O的切线,若BC=2,AB=4,则BD= . 科目:高中数学 来源: 题型:
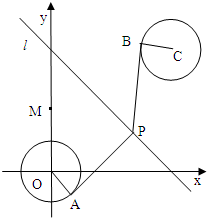 已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;
已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).
(2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).| 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;
(Ⅰ)将两圆方程相减可得一直线方程l:x+y-4=0,该直线叫做这两圆的“根轴”,试证点P落在根轴上;
(Ⅱ)求切线长|PA|的最小值;
 (Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
(Ⅲ)给出定点M(0,2),设P、Q分别为直线l和圆O上动点,求|MP|+|PQ|的最小值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省苏州市高三(上)期初数学试卷(解析版) 题型:解答题
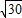 PO?若存在,指出有几个这样的点;若不存在,请说明理由;
PO?若存在,指出有几个这样的点;若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源:2011年江苏省盐城市高考数学二模试卷(解析版) 题型:解答题
 PO?若存在,指出有几个这样的点;若不存在,请说明理由;
PO?若存在,指出有几个这样的点;若不存在,请说明理由;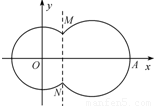
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com