
【题目】![]() 已知点F为抛物线E:
已知点F为抛物线E:![]() 的焦点,点A(2,m)在抛物线E上,且|AF|=3
的焦点,点A(2,m)在抛物线E上,且|AF|=3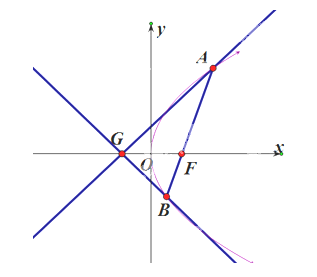 .
.
(1)求抛物线E的方程;
(2)已知点G(-1,0) , 延长AF交抛物线E于点B , 证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
【答案】
(1)
![]()
(2)
详见解析
【解析】解法一:(1)由抛物线的定义得|AF|=2+![]() .因为|AF|=3,即2+
.因为|AF|=3,即2+![]() =3,解得p=2,所以抛物线E的方程为
=3,解得p=2,所以抛物线E的方程为![]() =4x。
=4x。
(2)因为点A(2,m)在抛物线E:![]() =4x上,所以m=
=4x上,所以m=![]() ,由抛物线的对称性,不妨设A(2,
,由抛物线的对称性,不妨设A(2,![]() ). 由A(2,
). 由A(2,![]() ),F(1,0)得直线AF的方程式为y=
),F(1,0)得直线AF的方程式为y=![]() (x-1)。 由
(x-1)。 由![]() ,得
,得![]() , 解得x=2或x=
, 解得x=2或x=![]() ,从而B(
,从而B(![]() ,-
,-![]() ),又G(-1,0),所以
),又G(-1,0),所以![]() ,所以
,所以![]() +
+![]() =0,从而
=0,从而![]() AGF=
AGF=![]() BGF,这表明点F到直线GA,GB的距离相等。故以F为圆心且与直线GA相切的圆必与直线GB相切。
BGF,这表明点F到直线GA,GB的距离相等。故以F为圆心且与直线GA相切的圆必与直线GB相切。
解法二:(1)同解法一。
(2)设以点F为圆心且与直线GA相切的圆的半径为r。 因为点A(2,m)在抛物线E:![]() =4x上,所以m=
=4x上,所以m=![]() ,由抛物线的对称性,不妨设A(2,
,由抛物线的对称性,不妨设A(2,![]() ). 由A(2,
). 由A(2,![]() ),F(1,0)得直线AF的方程式为y=
),F(1,0)得直线AF的方程式为y=![]() (x-1)。 由
(x-1)。 由![]() ,得
,得![]() , 解得x=2或x=
, 解得x=2或x=![]() ,从而B(
,从而B(![]() ,-
,-![]() ),又G(-1,0),故直线GA的方程式为
),又G(-1,0),故直线GA的方程式为![]() ,从而
,从而![]() ,又GB的方程式为
,又GB的方程式为![]() ,所以点F到直线,GB的距离
,所以点F到直线,GB的距离![]() ,这表明以点F为圆心且与直线GA相切的圆必与直线GB相切。
,这表明以点F为圆心且与直线GA相切的圆必与直线GB相切。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(2015·四川)已知函数f(x)=-2(x+a)lnx+x2-2ax-2a2+a,其中a>0.
(1)设g(x)是f(x)的导函数,讨论g(x)的单调性;
(2)证明:存在a![]() (0,1),使得f(x)≥0,在区间(1,+
(0,1),使得f(x)≥0,在区间(1,+![]() )内恒成立,且f(x)=0在(1,+
)内恒成立,且f(x)=0在(1,+![]() )内有唯一解.
)内有唯一解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a,b 是函数![]() 的两个不同的零点,且a,b,-2 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q 的值等于( )
的两个不同的零点,且a,b,-2 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q 的值等于( )
A.6
B.7
C.8
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·北京)某校老年、中年和青年教师的人数见下表,采用分层抽样的方法调查教师的身体状况,在抽取的样本
中,青年教师有320人,则该样本的老年教师人数为( )
A.90
B.100
C.180
D.300
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)设函数![]() ,
,![]() 的定义域均为
的定义域均为![]() ,且
,且![]() 是奇函数,
是奇函数,![]() 是偶函数,
是偶函数,![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(Ⅰ)求![]() ,
,![]() 的解析式,并证明:当
的解析式,并证明:当![]() 时,
时,![]() ,
,![]() ;
;
(Ⅱ)设![]() ,
,![]() ,证明:当
,证明:当![]() 时,
时,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com